Метод доверительных интервалов разработан американским статистиком Ю.Нейманом, исходя из идей английского статистика Р.Фишера.
Нахождение границ доверительного интервала непосредственно зависит от закона распределения величины 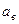 (это случайная величина), который, в свою очередь, определяется законом распределения случайной величины Х и, следовательно, зависит от его параметров (в частности, и от самого параметра а).
(это случайная величина), который, в свою очередь, определяется законом распределения случайной величины Х и, следовательно, зависит от его параметров (в частности, и от самого параметра а).
Ниже мы рассмотрим, как построить доверительный интервал для оценки математического ожидания М(х), среднего квадратического отклонения 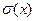 и вероятности события Р для известных законов распределения: нормального, биномиального.
и вероятности события Р для известных законов распределения: нормального, биномиального.
3. Доверительный интервал для оценки математического ожидания нормально распределенной случайной величины 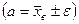
|
Пусть известно, что случайная величина Х имеет нормальное распределение, но неизвестен ее параметр а (математическое ожидание).
Допустим, что точечную оценку параметра а по выборочной средней 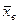 нашли, т.е.
нашли, т.е. 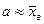 . Надо определить точность
. Надо определить точность 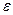 этой приближенной формулы при заданной надежности
этой приближенной формулы при заданной надежности 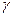 .
.
Эта задача решается в двух случаях: 1) когда параметр 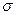 известен; 2) когда параметр
известен; 2) когда параметр 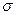 неизвестен.
неизвестен.
а) построение доверительного интервала для математического ожидания при известном 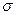 .
.
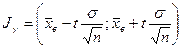 , (**)
, (**)
где: 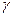 - заданная надежность (вероятность);
- заданная надежность (вероятность);
n – объем выборки;
t – значение аргумента функции Лапласа Ф(t), при котором 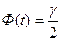 (см. приложение 2);
(см. приложение 2);
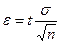 - точность оценки.
- точность оценки.
Исходя из обозначений для доверительного интервала нормально распределенной случайной величины имеем:
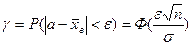 , где
, где 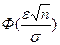 - функция Лапласа, значения которой приведены в приложении №2 Гмурман В.Е.
- функция Лапласа, значения которой приведены в приложении №2 Гмурман В.Е.
Если задана доверительная вероятность 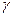 и объем выборки n, то из уравнения
и объем выборки n, то из уравнения 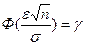 пользуясь таблицей Лапласа, можно найти значение аргумента
пользуясь таблицей Лапласа, можно найти значение аргумента 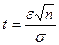 , а отсюда
, а отсюда 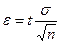 .
.
Величина t – случайная и при известном 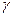 имеет нормальное распределение, как и случайная величина Х. Величина t определяет число средних квадратических отклонений
имеет нормальное распределение, как и случайная величина Х. Величина t определяет число средних квадратических отклонений 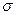 , которые надо отложить вправо и влево от центра рассеивания.
, которые надо отложить вправо и влево от центра рассеивания.
Заметим, что рассмотренную нами формулу (**) построения доверительного интервала для математического ожидания при известном 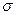 , можно использовать при достаточно больших n и в случае, если закон распределения не является нормальным. В этом случае
, можно использовать при достаточно больших n и в случае, если закон распределения не является нормальным. В этом случае 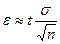 .
.
б) построение доверительного интервала для математического ожидания при неизвестном 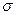 .
.
Пусть случайная величина Х – нормально распределена и 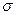 неизвестна. Тогда:
неизвестна. Тогда:
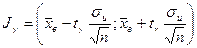 ,
,
где: 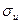 - (в Гмурмане В.Е. обозначается s) необходимо определить по формуле точечной оценки параметра
- (в Гмурмане В.Е. обозначается s) необходимо определить по формуле точечной оценки параметра 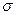 при
при 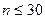 , т.е.
, т.е. 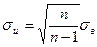 ;
;
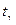 - находят по таблице приложения 3 (Гмурман В.Е.) по заданным n и
- находят по таблице приложения 3 (Гмурман В.Е.) по заданным n и 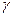 .
.
4. Доверительный интервал для оценки среднего квадратического отклонения нормально распределенной случайной величины 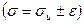 Допустим, что найдена точечная оценка для
Допустим, что найдена точечная оценка для 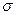 равная равная 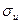 , т.е. , т.е. 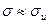 .
Требуется найти доверительный интервал .
Требуется найти доверительный интервал 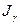 , накрывающий параметр , накрывающий параметр 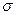 с надежностью с надежностью 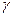 .
Потребуем выполнения соотношения .
Потребуем выполнения соотношения 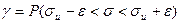 .
Преобразуем двойное неравенство .
Преобразуем двойное неравенство 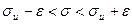 в равносильное неравенство в равносильное неравенство 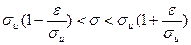 .
Обозначив .
Обозначив 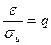 ,получим ,получим 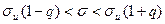 при при 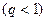 .
При .
При 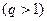 формула имеет вид формула имеет вид 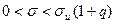 .
Для отыскания q составлена специальная таблица (см. приложение 4 Гмурман В.Е.).
Вычислив по выборке .
Для отыскания q составлена специальная таблица (см. приложение 4 Гмурман В.Е.).
Вычислив по выборке 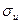 и определив по таблице значение q, получим искомый доверительный интервал: и определив по таблице значение q, получим искомый доверительный интервал: 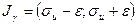 , где , где 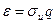 . .
|
| 4. Доверительный интервал для определения вероятности события Р (генеральной доли) при большом количестве опытов или большом объеме выборки |
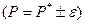 или в наших обозначениях предыдущей лекции
или в наших обозначениях предыдущей лекции 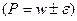 .
.
Точечной оценкой вероятности Р события служит частота 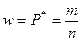 события. Для определения точности вычисления Р надо найти
события. Для определения точности вычисления Р надо найти 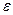 и записать
и записать 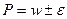 .
.
Величины 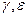 и n в этом случае связаны выражением:
и n в этом случае связаны выражением:
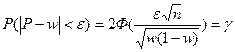 ,
,
где: 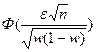 - функция Лапласа, значения которой см. в Приложении 2 Гмурман В.Е.;
- функция Лапласа, значения которой см. в Приложении 2 Гмурман В.Е.;
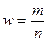 - частота появления события;
- частота появления события;
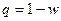 - частота не появления события.
- частота не появления события.
Замечание. Если величины m и n неизвестны, то принимают 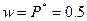 , так как
, так как 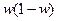 принимает максимальное значение при
принимает максимальное значение при 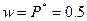 .
.
Замечание. Вы помните из прошлой лекции, что при больших n (порядка сотен) биномиальное распределение стремиться к нормальному.
Интервальной оценкой (с надежностью 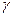 ) неизвестной вероятности Р биномиального распределения по относительной частоте w при больших n служит доверительный интервал:
) неизвестной вероятности Р биномиального распределения по относительной частоте w при больших n служит доверительный интервал:
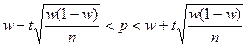 ,
,
где t – определяется по таблицам функции Лапласа (приложение 2) из соотношения 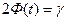 .
.
В этом случае для оценки генеральной доли Р нормально распределенного количественного признака по выборочной доле w будет использоваться формула:
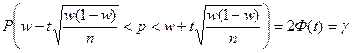 .
.
 2014-02-09
2014-02-09 740
740








