Таблица 1.1
| Размер обуви X | Число выданых пар ni /частота/ | Частость 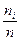 , n = 79 , n = 79 |
| х1 =36 | Pi =0.013 | |
| х2 = 37 | P2 = 0.013 | |
| х3 = 38 | P3 = 0.063 | |
| х4 = 39 | P4 = 0.101 | |
| Х5 = 40 | P5 = 0.215 | |
| х6 = 41 | P6 = 0.266 | |
| х7 = 42 | P7 = 0.288 | |
| х8 = 43 | P8 = 0.101 | |
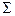 |
В таблице 1.1 введены значения Xi; случайной величины и соответствующие им частости, которые аналогичны вероятностям.
Пример 2. Построение вариационного ряда распределения.
Обследовано 1000 мужчин. Максимальный рост 188 см., минимальный 144 см. Для простоты вычисления все мужчины разбиты на 15 групп через равный интервал в 2 см. Число мужчин (частота) с ростом в заданном интервале обозначена через ni. Данные сведены в таблицу 1.2.
Таблица 1.2
| Рост | середина интервала X. | Число мужчин /частота/ ni | Частотность 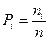 , n = 1000 , n = 1000 |
| 143-146 | х1 = 144,5 | р1 = 0.001 | |
| 146-149 | х2.= 147,5 | р2 = 0,002 | |
| 149-152 | , х3 = 150,5 | р3 = 0,008 | |
| 152-155 - | х4 = 153,5 | р4 = 0,026 | |
| 155-158 | х5 = 156,5 | р5 = 0,065 | |
| 158-161 ' | х6 = 159,5 | р6 = 0.12 | |
| 161-164 | . x7 = 162,5 | р7 = 0.181 | |
| 164-167 | х8 = 165,5 | р8 = 0,201 | |
| 167-170 | x9 = 168.5 | Р9 = 0,17 | |
| 170-173 | х10 = 171,5 | Р10 = 0,12 | |
| 173-176 | x11 = 174,5 | р11 = 0,064 | |
| 176-179 | х12 = 177,5 | Р12 = 0.028 | |
| 179-182 | х13 = 180,5 | Р13 = 0,01 | |
| 182-185 | x14 = 183,5 | р14 = 0.003 | |
| 185-188 | х15 = 186,5 | Р15 = 0,001 | |
| Итого 1000 | Итого 1 |
Переводя на язык теории вероятностей, получен ряд распределения случайной величины Х со значениями (х1, х2, …, х15) и соответствующими "вероятностями" (Р1, Р2, …, Р15).
Графическое изображение вариационного ряда соответствует графическому изображению дискретной случайной величины (многоугольник распределения) и называется полигоном распределения.
Тема 13: «Математическая статистика».
Время: 2 часа
Цель лекции: Ознакомить слушателей с интервальными оценками параметров распределения случайных величин.
Учебные вопросы:
· Интервальные оценки параметров распределения.
· Доверительный интервал для оценки математического ожидания случайной величины, обладающей свойствами нормального распределения (при известном и неизвестном среднем квадратическом отклонении).
· Оценка вероятностей.
· Показать различие между оценками числовых характеристик (математическая статистика) и самими числовыми характеристиками (теория вероятностей).
1. Понятие об оценках параметров
На предыдущей лекции мы узнали, что если случайная величина изучается по выборке, то находят оценки параметров (точечные) (Хср, D (x), s (х)), то есть их приближенные значения. Чем больше объем выборки п, тем точнее оценки параметров. Причем, если мы будем рассматривать несколько выборок из одной и той же генеральной совокупности, и для каждой выборки найдем оценки Хср, то есть `х 1, `х 2,..., `хk, то они обладают свойством статистической устойчивости, то есть группируются около некоторого числа, которое и принимают за М (х).
Итак, для большого объема выборки 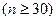 оценки параметров (Хср, D (x), s (х)) определяются по формулам, данным в предыдущей лекции. Если объем выборки небольшой
оценки параметров (Хср, D (x), s (х)) определяются по формулам, данным в предыдущей лекции. Если объем выборки небольшой 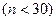 , то считают исправленную дисперсию и среднее квадратическое отклонение:
, то считают исправленную дисперсию и среднее квадратическое отклонение:
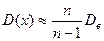 ,
, 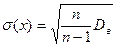 .
.
Сегодня мы рассмотрим интервальные оценки параметров распределения и введем понятие о доверительном интервале и доверительной вероятности.
Допустим, что для изучения некоторой случайной величины Х (признака генеральной совокупности) необходимо по статистическим данным произвести оценку неизвестного параметра а (это может быть Хср, D (x), s (х) или р) с определенной степенью точности и надежности, т.е. надо указать границы, в которых практически достоверно лежит этот неизвестный параметр а.
Это означает, что надо найти такую выборочную оценку 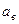 для искомого параметра а, при которой с наименьшей вероятностью (надежностью) будет выполняться неравенство:
для искомого параметра а, при которой с наименьшей вероятностью (надежностью) будет выполняться неравенство:
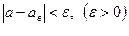 . (*)
. (*)
Отсюда видно, что чем меньше 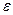 , тем точнее характеризуется неизвестный параметр а с помощью выборочной оценки
, тем точнее характеризуется неизвестный параметр а с помощью выборочной оценки 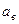 . Следовательно, число
. Следовательно, число 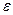 характеризует точность оценки параметра а.
характеризует точность оценки параметра а.
Надежность выполнения неравенства (*) оценивается числом 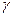 , которое называют доверительной вероятностью:
, которое называют доверительной вероятностью:
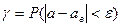 .
.
Итак, число 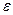 - характеризует точность оценки параметра а;
- характеризует точность оценки параметра а;
число 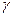 - характеризует н адежность оценки параметра а.
- характеризует н адежность оценки параметра а.
В практических задачах либо заранее задается надежность 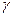 и надо найти точность оценки, либо, наоборот, задается точность
и надо найти точность оценки, либо, наоборот, задается точность 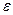 , а требуется найти надежность оценки.
, а требуется найти надежность оценки.
Как правило доверительную вероятность 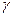 задают числом, близким к единице: 0,95; 0,97; 0,99; 0,999.
задают числом, близким к единице: 0,95; 0,97; 0,99; 0,999.
2. Понятие о доверительном интервале
Заменим неравенство 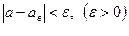 равносильным ему двойным неравенством
равносильным ему двойным неравенством 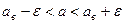 .
.
Тогда доверительную вероятность можно записать в виде:
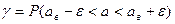 .
.
Определение. Интервал 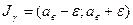 , который с заданной доверительной вероятностью (надежностью)
, который с заданной доверительной вероятностью (надежностью) 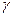 накрывает (включает) оцениваемый параметр а, называют доверительным интервалом.
накрывает (включает) оцениваемый параметр а, называют доверительным интервалом.
Очевидно, что чем больше требуется точность 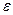 (т.е., чем меньше длина интервала), тем меньше вероятность накрыть интервалом
(т.е., чем меньше длина интервала), тем меньше вероятность накрыть интервалом 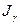 искомый параметр а, и наоборот, с уменьшением точности
искомый параметр а, и наоборот, с уменьшением точности 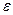 (увеличением длины интервала) увеличивается надежность
(увеличением длины интервала) увеличивается надежность 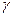 накрыть интервалом
накрыть интервалом 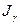 параметр а.
параметр а.
 2014-02-09
2014-02-09 1147
1147
