Виды вариационных рядов

ВАРИАЦИОННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ

Обычно полученные наблюдаемые данные представляют собой множество расположенных в беспорядке чисел.

. Операция, заключающаяся в том, что результаты наблюдений над случайной величиной располагают в порядке неубывания, называется ранжированием опытных данных.

После проведения операции ранжирования опытные данные нетрудно объединить в группы, т.е. сгруппировать так, что в каждой отдельной группе значения случайной величины будут одинаковы.

Определение. Значения признака, которые при переходе от одного элемента совокупности (группы) к другому изменяются (варьируют), называются вариантами и обычно обозначаются малыми латинскими буквами х, у, z.

Порядковый номер варианта (значения признака) называется рангом: x₁ - 1-й вариант (1-е значение признака), x₂ - 2-й вариант (2-е значение признака), x_i – i-й вариант (i- е значение признака).

Определение. Численность отдельной группы сгруппированного ряда наблюдаемых данных называется частотой или весом соответствующего варианта и обозначается n_i, где i – индекс варианта.

Частота (n_i) показывает, сколько раз встречается тот или иной вариант (значение признака) в статистической совокупности.

Определение. Отношение частоты данного варианта к общей сумме частот всех вариантов называется частостью или долей этого варианта.

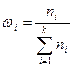, где k – число вариантов.

Частость или относительная частота (w_i) показывает, какая часть единиц совокупности имеет тот или иной вариант. Нетрудно заметить, что частость w_i является статистической вероятностью появления варианта.

Сумма всех частостей равна 1:

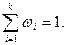
Вариационные ряды бывают дискретными и интервальными.

Определение. Дискретным вариационным рядом распределения называется ранжированная (в порядке возрастания или убывания) совокупность вариантов с соответствующими им частотами (весами) или частостями.

Дискретные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга не менее чем на некоторую конечную величину. В дискретных вариационных рядах задаются точечные значения признака. Общий вид дискретного вариационного ряда показан в табл. 1.

Таблица 1

Значения признака (xi)	x1	x2	…	xn
Частость (wi)	w1	w2	...	wk

Дискретный вариационный ряд графически можно представить с помощью полигона распределения частот или частостей.

Определение. Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частостями попаданий в каждый из них значений величины.

Интервальные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга на сколь угодно малую величину. Значения признака в них задаются в виде интервалов. Общий вид интервального вариационного ряда показан в табл. 2, где i = 1,2,…,k

Таблица 2.

Значения признака (хi)	a1 – a2	a2 – a3	…	ai-1 – ai
Частость (wi)	w1	w2	...	wk

В интервальных вариационных рядах в каждом интервале выделяют верхнюю и нижнюю границы. Разность между верхней и нижней границами интервала называется интервальной разностью или размахом вариации R.

.

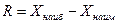Чтобы ряд не был громоздким, обычно число интервалов берут от 7 до 11. Для более точного определения величины частичного интервала можно воспользоваться формулой Стерджеса:

.

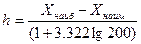Промежуточные интервалы получают, прибавляя к концу предыдущего интервала длину частичного интервала h. Кроме того, в интервальном вариационном ряде могут встречаться интервалы разной длины.

Определение. Если интервалы в вариационном ряде имеют одинаковую длину (интервальную разность), их называют равновеликими, в противном случае – неравновеликими.

Частоты в каждом интервале называют интервальными, а их отношение к общему числу наблюдений – интервальными частостями. При вычислении интервальных частостей округление результатов следует проводить таким образом, чтобы общая сумма частостей была равна 1.

Интервальные вариационные ряды графически можно представить с помощью гистограммы, т.е. столбчатой диаграммы. Если же интервалы имеют разную величину, по оси ординат необходимо откладывать значения абсолютной или относительной плотности распределения.

Определение. Абсолютная плотность – отношение частоты интервала к его величине:

.

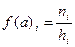Определение. Относительная плотность – отношение частости интервала к его величине:

.

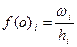Иногда интервальный вариационный ряд для простоты исследований условно заменяют дискретным. В этом случае серединное значение i- го интервала принимают за вариант X_i, а соответствующую интервальную частоту n_i – за частоту этого интервала.

Например, требуется обследовать большой коллектив рабочих одной и той же профессии. Из за трудоемкости всей работы делается выборочное исследование части этого коллектива.

Весь коллектив при этом называется генеральной совокупностью, а выделенная для обследования часть коллектива называется выборочной совокупностью.

Отношение объема выборочной совокупности n, к объему генеральной совокупности N,т.е. 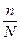называется относительным показателем выборки.

Любое выборочное наблюдение, как правило, не дает точные характеристики всей генеральной совокупности. Поэтому, каждый результат, вычисленный по данным выборки, имеет некоторую погрешность. Эта погрешность называется ошибкой репрезентативности.

Рассмотрим на примере систематизацию полученных данных.

Пример 1. При регистрации размеров выдаваемой на складе имущества мужской обуви были получены следующие данные о 79 выдачах, которые были сведены в таблицу 1.1. по возрастающему значению признака / размера обуви /.