Задано эмпирическое распределение непрерывной случайной величины X в виде последовательности интервалов 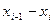 и соответствующих им частот
и соответствующих им частот 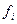 , причем
, причем 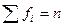 (объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина Х распределена равномерно.
(объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина Х распределена равномерно.
Правило. Для того, чтобы проверить гипотезу о равномерном распределении X по закону
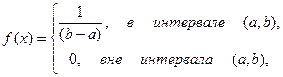
надо:
1. Оценить параметры a и b – концы интервала, в котором наблюдались возможные значения X, по формулам (через 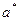 и
и 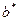 обозначены оценки параметров):
обозначены оценки параметров):
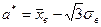 ,
, 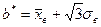 .
.
2. Найти плотность вероятности предполагаемого распределения
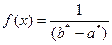 .
.
3. Найти теоретические частоты:
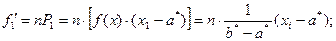

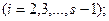
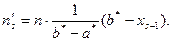
4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы 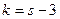 , где s – число интервалов, на которые разбита выборка.
, где s – число интервалов, на которые разбита выборка.
4. Проверка гипотезы о распределении генеральной совокупности по закону Пуассона.
Задано эмпирическое распределение дискретной случайной величины X. Требуется, используя критерий Пирсона, проверить гипотезу о распределении генеральной совокупности по закону Пуассона.
Правило. Для того, чтобы при уровне значимости 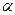 проверить гипотезу о том, что дискретная случайная величина Х распределена по закону Пуассона, надо:
проверить гипотезу о том, что дискретная случайная величина Х распределена по закону Пуассона, надо:
1. Найти по заданному эмпирическому распределению выборочную среднюю 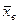 ;
;
2. Принять в качестве оценки параметра 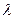 распределения Пуассона выборочную среднюю
распределения Пуассона выборочную среднюю 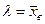 .
.
3. Найти по формуле Пуассона (или по готовым таблицам) вероятности 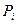 появления ровно i событий в n испытаниях (i = 0,1,2,…,r, где r – максимальное число наблюдавшихся событий; n – объем выборки).
появления ровно i событий в n испытаниях (i = 0,1,2,…,r, где r – максимальное число наблюдавшихся событий; n – объем выборки).
4. Найти теоретические частоты по формуле 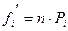 .
.
5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы 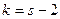 , где s – число различных групп выборки (если производилось объединение малочисленных частот в одну группу, то s – число оставшихся групп выборки после объединения частот).
, где s – число различных групп выборки (если производилось объединение малочисленных частот в одну группу, то s – число оставшихся групп выборки после объединения частот).
 2014-02-09
2014-02-09 4780
4780
