Применение средств дифференциального исчисления при разработке тактики коммерческой фирмы
В экономической деятельности часто возникает необходимость поиска оптимальных (предпочтительных в некотором смысле) решений. Как правило, оптимальность предполагает обеспечение max (максимума) или min (минимума) оптимизируемых показателей. Так, в условиях рыночной экономики, коммерческая фирма оптимизирует свою деятельность по основным ее показателям: по уровням затрат Z, по цене р на товар, по объему продаж х.
Критериями оптимизации, являются: максимум общей выручки W (х) от продаж maxW (х), максимум дохода П (х) от продаж maxП (x), минимум затрат Z (x): minZ (x), и т.д.
Рассмотрим простейшие оптимизационные задачи, описывающие тактику коммерческой фирмы для двух моделей рынка: для условий монопольной торговли и условий совершенной конкуренции.
В качестве исходных данных будем использовать функцию издержек Z (х), функцию цены р (х) от спроса на товар (в условиях монопольной конкуренции), равновесную рыночную цену р о (в условиях совершенной конкуренции). При этом учтем экономический характер перечисленных функций. Функция издержек является возрастающей, т.к. с увеличением объема продаж, расходы по его реализации растут. Различают постоянные затраты, не зависящие от объема продаж х (плата за аренду, зарплата управленческого персонала и т.п.) и условно переменные затраты, зависящие от объема продаж х (расходы на закупку товара, топливо, зарплату продавцов и т.п.). Перечисленным условиям удовлетворяют следующие модели издержек Z (x).
|
|
|
I Линейная модель
 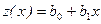
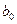
| II Квадратичнаямодель
 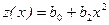
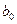
| Здесь 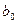 - постоянные затраты, - постоянные затраты, 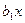 и и 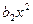 - условно переменные затраты, которые, при реализации единицы продукции остаются постоянными в модели I, и возрастают с ростом объема продаж в модели II. - условно переменные затраты, которые, при реализации единицы продукции остаются постоянными в модели I, и возрастают с ростом объема продаж в модели II.
|
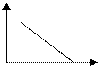
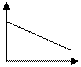
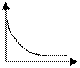
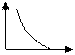
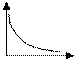
Согласно закона понижающегося спроса: по мере увеличения цены товара р спрос х на данный товар снижается. Поэтому функция р (х) является монотонно убывающей.
Линейная модель 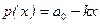
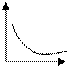
| Гиперболическая модель (в этих моделях 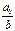 - предельная цена товара) - предельная цена товара)
| |
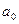 х
х х
х 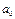 р р
|   со сдвигом со сдвигом 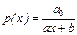
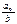 х
х р х
х р
|   без сдвига без сдвига 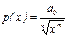 , , 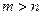 р х
х р
р х
х р
|
 2014-02-09
2014-02-09 482
482








