§ 1 Экономический смысл производной Математический аппарат дифференциального исчисления широко используется в курсе современного экономического анализа. Всякая экономическая деятельность осуществляется для достижения некоторого результата у и требует приложения определенных усилий х. Пусть зависимость между усилием х и результатом у описывается функцией у = f (х) непрерывной на некотором промежутке Х.
Изменение усилий х на величину 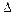 х
х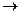 0 приводит к изменению результата у на величину ∆у (х) =f (х+∆х) -f (х).
0 приводит к изменению результата у на величину ∆у (х) =f (х+∆х) -f (х).
Разностное отношение 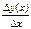 представляет собой среднюю эффективность усилий у, прилагаемых на уровнях. Предельную эффективность рассматриваемого экономического процесса на уровне х найдем, перейдя к пределу представляет собой среднюю эффективность усилий у, прилагаемых на уровнях. Предельную эффективность рассматриваемого экономического процесса на уровне х найдем, перейдя к пределу  . Т.о., предельная эффективность на уровне усилий х вычисляется как производная результата: . Т.о., предельная эффективность на уровне усилий х вычисляется как производная результата: 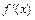 . . |  у f (х+∆х) ∆ у f (х) х х+∆х х у f (х+∆х) ∆ у f (х) х х+∆х х |
Пример 1. Пусть функция U = U (t) выражает количество произведенной продукции за время t. Найдем производительность труда в момент времени t 0.
|
|
|
За период времени [ t 0; t 0+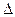 t ] производительность труда изменится на величину
t ] производительность труда изменится на величину 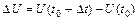 и средняя производительность Zср труда за интервал времени
и средняя производительность Zср труда за интервал времени 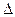 t составит
t составит  .
.
Производительность труда Z в момент времени t 0 найдем как предельное значение средней производительности Zср при 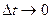 :
: 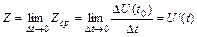 .
.
Пример 2. Пусть х – объем выпущенной продукции, а у – затраты на её производство, тогда 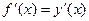 описывает предельные издержки производства при заданном объеме х выпускаемой продукции.
описывает предельные издержки производства при заданном объеме х выпускаемой продукции.
Пример 3. Пусть х – количество потребленного человеком блага, а у – полезность этого баланса, тогда  представляет собой предельную полезность этого баланса на заданном уровне х его потребления.
представляет собой предельную полезность этого баланса на заданном уровне х его потребления.
Пример 4. Пусть х – объем продаж, а у – общая выручка от продажи, тогда  характеризует предельную выручку на уровне продаж х.
характеризует предельную выручку на уровне продаж х.
 Аналогичным образом определяются предельный доход, предельный продукт и др. предельные величины. Применение дифференциального исчисления к исследованию экономических явлений на основе анализа соответствующих предельных величин называется предельным анализом. Предельные величины характеризуют не состояние (как суммарная или средняя величина), а процесс изменения экономического явления. При этом производная
Аналогичным образом определяются предельный доход, предельный продукт и др. предельные величины. Применение дифференциального исчисления к исследованию экономических явлений на основе анализа соответствующих предельных величин называется предельным анализом. Предельные величины характеризуют не состояние (как суммарная или средняя величина), а процесс изменения экономического явления. При этом производная  выступает как скорость изменения некоторого экономического явления во времени или относительно другого экономического фактора.
выступает как скорость изменения некоторого экономического явления во времени или относительно другого экономического фактора.
В экономической литературе предельные величины называют маржинальными. При их записи к обычному обозначению величин добавляется буква М. При записи средних величин добавляется буква А. (от англ. Average – средняя). Например, МК – предельный доход; АК – средний доход.
§ 2 Соотношения между средним и предельным доходами в условиях монопольного и конкурентного рынков Пусть произведена продукция в объеме q, и p – цена единицы продукции. Тогда доход (выручка) D от реализации произведенной продукции составляет: D = pq.
|
|
|
В условия монополии полностью контролируется предложение, а значит и цена p продукции. При этом, как правило, с увеличением цены p спрос на продукцию падает. Предположим, эта тенденция описывается линейным законом p=aq+b, (a< 0 ,b> 0 ). Тогда суммарный доход D от реализованной продукции составит: 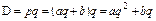 , cредний доход составит: , cредний доход составит: 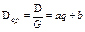 , а предельный доход, т.е. дополнительный доход от реализации дополнительной продукции, составит , а предельный доход, т.е. дополнительный доход от реализации дополнительной продукции, составит 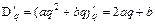 . Т.о., в условиях монопольного рынка с ростом количества . Т.о., в условиях монопольного рынка с ростом количества |  D D D D   0 0  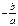 |
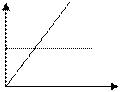 реализованной продукции предельный доход снижается, что приводит к уменьшению среднего дохода.
реализованной продукции предельный доход снижается, что приводит к уменьшению среднего дохода.
Рассмотрим монопольный (конкурентный) рынок. В условиях совершенной конкуренции продажа товаров в основном осуществляется по рыночной цене, например, p = b. Тогда суммарный доход составит D = bq, средний доход 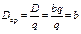 , предельный доход , предельный доход 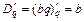 (средний и предельный доходы совпадают). (средний и предельный доходы совпадают). | D D (суммарный доход) Dср (средний доход) 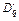 (предельный доход) 0 q (предельный доход) 0 q |
 2014-02-09
2014-02-09 1879
1879
