Функции находят широкое применение в экономической теории и практике. Спектр использования разнообразных функций: от простейших линейных до функций, полученных по определённому алгоритму с помощью программ, рекуррентных соотношений, связывающих состояния изучаемых объектов в разные периоды времени. На ряду с линейными используются нелинейные монотонные функции, моделирующие характер тенденции экономического процесса (возрастания, убывания, и т.д.). Периодичность экономического процесса позволяет учесть тригонометрические модели.
 Часто в экономическом процессе удаётся выделить основной фактор, определяющий тип тенденции, а действием побочных факторов пренебречь (или зафиксировать побочные факторы на одном уровне), тогда влияние основного фактора изучается с помощью функции одной переменной
Часто в экономическом процессе удаётся выделить основной фактор, определяющий тип тенденции, а действием побочных факторов пренебречь (или зафиксировать побочные факторы на одном уровне), тогда влияние основного фактора изучается с помощью функции одной переменной 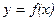 , где x - независимая (факторная) переменная, y - зависимая (результативная) переменная. y
, где x - независимая (факторная) переменная, y - зависимая (результативная) переменная. y
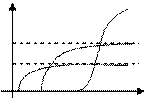
Пример 1. Зависимость спроса y на разные товары от дохода x описывается функциями Л. Торнквиста: 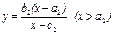 , , 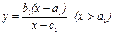 , , 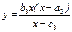 , где а 1, а 2, а 3 – уровни дохода, при которых начинается потребление тех или иных товаров; b 1, b 2 – уровни насыщения для групп товаров первой и второй необходимости. , где а 1, а 2, а 3 – уровни дохода, при которых начинается потребление тех или иных товаров; b 1, b 2 – уровни насыщения для групп товаров первой и второй необходимости. | b 2 b 1 0 а 1 а 2 а 3 x |
| Пример 2. Рассматривая в одной системе координат кривую спроса и кривую предложения, можно установить равновесную точку p 0 - рыночную цену товара, формируемую в условиях конкурентного рынка. | 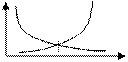 кривая кривая спроса предложения p 0 кривая кривая спроса предложения p 0 |
Пример 3. Пусть 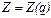 - функция издержек (полных затрат) фирмы; - функция издержек (полных затрат) фирмы; 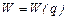 - функция дохода от объёма производства q. Тогда прибыль - функция дохода от объёма производства q. Тогда прибыль 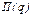 при данном производстве составляет при данном производстве составляет 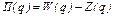 . И можно установить уровни объёма производства, при которых это производство приносит прибыль . И можно установить уровни объёма производства, при которых это производство приносит прибыль 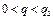 , , 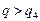 , или же производство убыточно , или же производство убыточно 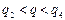 , или даёт максимальную прибыль , или даёт максимальную прибыль 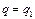 или максимальный убыток или максимальный убыток 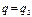 и найти их размеры. и найти их размеры. |  у у 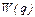 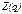 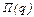 0 q 1 q 2 q 3 q 4 0 q 1 q 2 q 3 q 4 |
 2014-02-09
2014-02-09 2165
2165