Задача 1 Провести анализ математической модели тактики коммерческой фирмы-монополиста на рынке товаров, если функция цены р от спроса х имеет вид 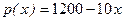 , а затраты по реализации товара описывается функцией издержек
, а затраты по реализации товара описывается функцией издержек 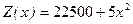 , где х - объем продаж. Выполнить задания:
, где х - объем продаж. Выполнить задания:
а) найти оптимальные значения объема продаж 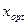 и цены товара
и цены товара 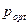 , обеспечивающие максимум общей выручки от продаж, оценить величину maxW (x);
, обеспечивающие максимум общей выручки от продаж, оценить величину maxW (x);
б) определить интервалы значений объемов продаж х, в которых деятельность коммерческой фирмы будет прибыльной (убыточной);
в) найти оптимальные значения объема продаж 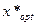 и цены товара
и цены товара 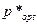 , обеспечивающие коммерческой фирме максимум дохода от продаж maxП (х), найти maxП (х);
, обеспечивающие коммерческой фирме максимум дохода от продаж maxП (х), найти maxП (х);
г) дать геометрическую инерпретацию полученных выше результатов.
Решение а) Найдем функцию общей выручки 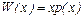 , имеем
, имеем 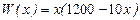 . Тогда предельная выручка при объеме продаж х составляет
. Тогда предельная выручка при объеме продаж х составляет 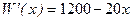 . Для нахождения оптимального объема продаж
. Для нахождения оптимального объема продаж 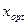 решим уравнение
решим уравнение 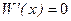 ,
, 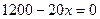 , откуда получаем х = 60.
, откуда получаем х = 60.
Заметим, что 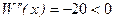 , следовательно в точке х = 60 функция выручки W (x) имеет максимальное значение и
, следовательно в точке х = 60 функция выручки W (x) имеет максимальное значение и 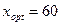 - оптимальный объем продаж. Тогда
- оптимальный объем продаж. Тогда 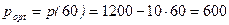 р. - оптимальная цена единицы товара и
р. - оптимальная цена единицы товара и 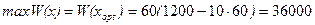 р. - максимальная общая выручка.
р. - максимальная общая выручка.
б) Деятельность коммерческой фирмы будет прибыльной при объемах продаж х, удовлетворяющих условию 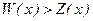 . Найдем точки безубыточности, решив уравнение
. Найдем точки безубыточности, решив уравнение 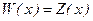 . Имеем
. Имеем 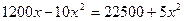 ,
,
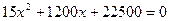 ,
, 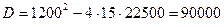 ,
, 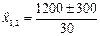 ,
, 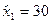 ,
, 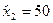 .
.
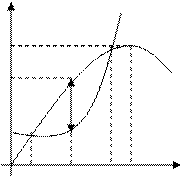 При объеме продаж
При объеме продаж 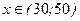 фирма будет получать доход
фирма будет получать доход 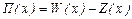 , при объемах продаж
, при объемах продаж 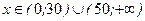 деятельность фирмы убыточна.
деятельность фирмы убыточна.
в) Для определения оптимальных объема продаж 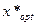 и цены товара и цены товара 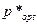 , обеспечивающих фирме максимум дохода , обеспечивающих фирме максимум дохода 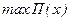 , найдем решение уравнения , найдем решение уравнения 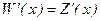
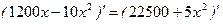 , , 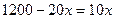 .
При этом .
При этом 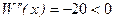 , , 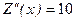 , т.е. , т.е. 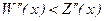 - при любом объеме продаж х, в том числе и при х = 40, тогда - при любом объеме продаж х, в том числе и при х = 40, тогда 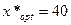 и и
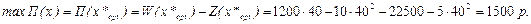
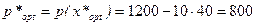 р. р.
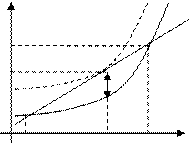
| W (x) Z (x) 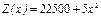
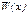 0
0 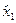 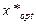 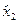 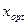 х
30 40 50 60 х
30 40 50 60
|
Т.о., при продаже 40 единиц товара по цене 800 р. фирма получит максимальный доход в размере 1500 р.
Задача 2 Провести анализ математической модели тактики коммерческой фирмы в условиях совершенной конкуренции, если равновесная рыночная цена составляет р о = 700 р., а издержки фирмы по реализации товара описывается функцией 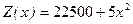 .
.
а) Определить интервалы значений объемов продаж, при которых деятельность фирмы будет прибыльной (убыточной). Найти оптимальный объем продаж 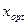 ,обеспечивающий фирме максимум дохода.
,обеспечивающий фирме максимум дохода.
б) Определить, при каких значениях параметра 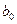 функции издержек
функции издержек 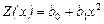 фирма будет иметь убытки при любых объемах продаж х. Представить полученные результаты графически.
фирма будет иметь убытки при любых объемах продаж х. Представить полученные результаты графически.
в) При каких значениях рыночной цены р о фирма будет иметь прибыль хотя бы при некоторых объемах продаж.
г) При каких значениях параметра 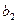 фирма будет иметь доходы хотя бы при не которых объемах продаж.
фирма будет иметь доходы хотя бы при не которых объемах продаж.
Решение а) Интервал прибыльности продаж найдем из условия 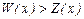 . Учтем, что в условиях совершенной конкуренции
. Учтем, что в условиях совершенной конкуренции 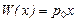 , тогда имеем
, тогда имеем 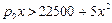 .
.
Найдем координаты точек безубыточности, как корни уравнения 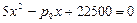 или
или 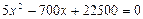 ,
,
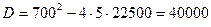 ,
, 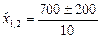 ,
, 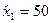 ,
, 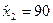 .
.
Т.о., при объемах продаж 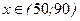 фирма будет получать доходы, а при объемах продаж фирма будет получать доходы, а при объемах продаж 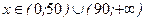 деятельность фирмы является убыточной. Найдем оптимальный объем продаж деятельность фирмы является убыточной. Найдем оптимальный объем продаж 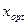 , беспечивающий максимальный доход , беспечивающий максимальный доход 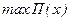 из условия из условия 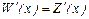 , имеем , имеем 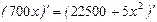 , , 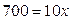 , х = 70.
Т.к. , х = 70.
Т.к. 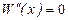 , , 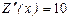 , то , то 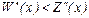 при х = 70, тогда при х = 70, тогда 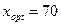 . Т.о., при объеме продаж . Т.о., при объеме продаж 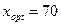 по рыночной цене р о = 700 р. коммерческая фирма получит максимальный доход в размере по рыночной цене р о = 700 р. коммерческая фирма получит максимальный доход в размере
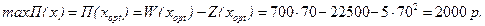
|  W (x) Z (x) W (x) Z (x) 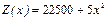 49000
49000 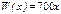 0
0 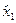 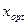 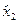 х
5 0 70 90 х
5 0 70 90
|
б) Если при любых объемах продаж выполняется условие 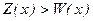 или
или 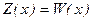 лишь в одной точке, фирма будет иметь только убытки. В этом случае квадратное уравнение
лишь в одной точке, фирма будет иметь только убытки. В этом случае квадратное уравнение 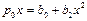 должно иметь не более одного корня, что возможно, когда
должно иметь не более одного корня, что возможно, когда 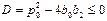 ,
, 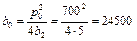 . Т.о., фирма имеет убытки при любых объемах продаж х, если ее условно постоянные затраты
. Т.о., фирма имеет убытки при любых объемах продаж х, если ее условно постоянные затраты 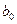 превысят или достигнут значение 24500 р.
превысят или достигнут значение 24500 р.
в) Фирма будет иметь прибыль хотя бы при некоторых объемах продаж, если уравнение 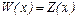 имеет два корня, т.е. имеет два корня, т.е. 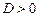 . Проверим выполнение этого условия . Проверим выполнение этого условия 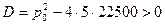 , откуда , откуда 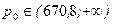 . .
| 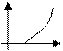  670,8
670,8 
|
г) Фирма будет иметь доходы хотя бы при не которых объемах продаж, если 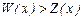 , т.е.
, т.е. 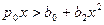 ,
,
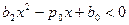 ,
, 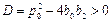 ,
, 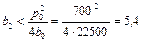 .
.
Фирма будет иметь доходы при 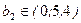 , терпит убыток при
, терпит убыток при 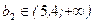 .
.
 2014-02-09
2014-02-09 756
756








