Классификация тенденций экономических процессов
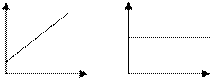 При решении задач экономики часто необходимо анализировать тенденции экономических показателей. Рассмотрим разные варианты изменения переменной у при увеличении факторной переменной х с учетом двух признаков: направления изменения величины
При решении задач экономики часто необходимо анализировать тенденции экономических показателей. Рассмотрим разные варианты изменения переменной у при увеличении факторной переменной х с учетом двух признаков: направления изменения величины 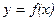 и направления изменения предельной величины зависимой переменной
и направления изменения предельной величины зависимой переменной 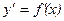 . y
. y 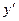
I Тенденция возрастания с постоянной скоростью может быть описана линейным уравнением 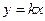 или или 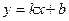 , , 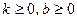 . Тогда скорость возрастания y равна . Тогда скорость возрастания y равна 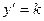 - постоянна и неотрицательна. - постоянна и неотрицательна. | k b x x |
Пример 1 Стоимость покупки 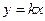 возрастает с постоянной скоростью k (цена продукта) по мере увеличения веса х покупаемого продукта.
возрастает с постоянной скоростью k (цена продукта) по мере увеличения веса х покупаемого продукта.
 Пример 2 Если затраты от реализации единицы товара постоянны и не зависят от объема реализации x, то совокупные издержки
Пример 2 Если затраты от реализации единицы товара постоянны и не зависят от объема реализации x, то совокупные издержки 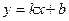 и суммируются из kx - издержек от реализации товара в объеме x и b - постоянных издержек.
и суммируются из kx - издержек от реализации товара в объеме x и b - постоянных издержек.
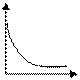
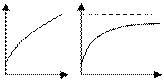
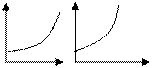
II Тенденции возрастания с постоянно убывающей скоростью описывается выпуклой вверх возрастающей кривой 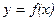 , которая либо , которая либо 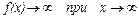 , либо , либо  . При этом производная . При этом производная 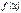 монотонно убывает с ростом x. монотонно убывает с ростом x. | у 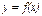 А А  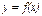 х х х х х х |
Математические модели: 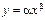 (
(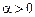 ,
, 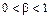 ) – степенная модель,
) – степенная модель,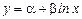 (
( ) – логарифмическая модель,
) – логарифмическая модель, 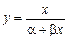 - дробно-рациональная модель.
- дробно-рациональная модель.
Пример 1 Закон убывающей предельной полезности (Д. Бернулли 1788 г.): совокупная полезность U с ростом объема x потребляемого блага возрастает с монотонно убывающей скоростью.
 Пример 2 Закон убывающей доходности ресурсов: по мере увеличения количества используемого в производстве переменного ресурса k при неизменном уровне других фиксированных ресурсов неизбежно наступает момент, когда по мере увеличения k прирост продукции
Пример 2 Закон убывающей доходности ресурсов: по мере увеличения количества используемого в производстве переменного ресурса k при неизменном уровне других фиксированных ресурсов неизбежно наступает момент, когда по мере увеличения k прирост продукции 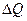 , приходящийся на очередную порцию
, приходящийся на очередную порцию 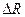 используемого ресурса будет монотонно снижаться.
используемого ресурса будет монотонно снижаться.
III Тенденция возрастания с монотонно возрастающей скоростью описывается вогнутой возрастающей кривой 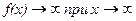 , при этом , при этом  . Математические модели: . Математические модели: 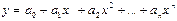 - полиномиальная, - полиномиальная, | у 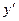 х х х х |
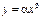 (
(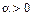 ,
, 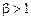 ) – степенная,
) – степенная, 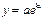 (
( ,
, 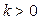 ) – экспоненциальная. Особенность экспоненциальной модели в следующем:
) – экспоненциальная. Особенность экспоненциальной модели в следующем: 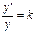 - не зависит от аргумента х. Отношение
- не зависит от аргумента х. Отношение 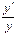 называют темпом роста.
называют темпом роста.
 Пример Закон спроса: в условиях монопольного рынка при увеличении объема продаж х совокупная выручка W возрастает с монотонно возрастающей скоростью. y
Пример Закон спроса: в условиях монопольного рынка при увеличении объема продаж х совокупная выручка W возрастает с монотонно возрастающей скоростью. y 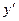
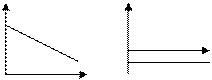
IV Тенденция убывания с постоянной скоростью может быть описана линейным уравнением 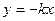 или или 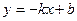 , , 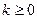 , , 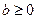 . Тогда скорость возрастания y равна . Тогда скорость возрастания y равна 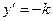 - неотрицательная постоянная. - неотрицательная постоянная. | b k x |
Пример 1 Закон спроса: спрос D на товар линейно падает с ростом цены р на этот товар.
Пример 2 Линейная модель амортизации: текущая стоимость у средств производства линейно убывает с ростом срока х эксплуатации средств производства 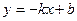 , где b - исходная стоимость средств производства.
, где b - исходная стоимость средств производства.
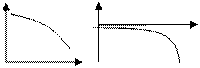
V Тенденция убывания с монотонно убывающей скоростью описывается убывающей вогнутой кривой, имеющей горизонтальную асимптоту 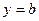 , , 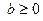 . . 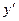 монотонно убывает по абсолютной величине с ростом х. Математические модели: монотонно убывает по абсолютной величине с ростом х. Математические модели: 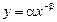 ( (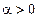 , , 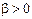 ) – степенная модель, ) – степенная модель, | 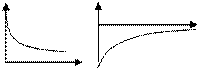 у у 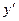 х х х х |
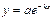 (
(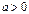 ,
, 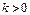 ) – экспоненциальная модель с постоянным темпом
) – экспоненциальная модель с постоянным темпом 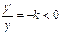 ,
, 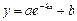 (
(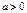 ,
,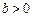 ,
, 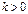 ) – экспоненциальная модель с горизонтальной асимптотой,
) – экспоненциальная модель с горизонтальной асимптотой, 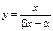 (
(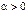 ,
,  ) - дробно-рациональная модель.
) - дробно-рациональная модель.
Пример 1 Закон убывающей предельной полезности: предельная полезность (полезность последней порции потребленного блага) монотонно убывает с ростом общего объема х потребленного блага.
Пример 2. Спрос D на товар монотонно падает с ростом цены р.
 Пример 3. Всякая система (коллектив, организм, устройство и т.п.) при заданных условиях деятельности имеет определенную продуктивность (производительность) П. Воздействие на систему с целью повышения её продуктивности называется стимуляцией системы. Принцип убывающей отдачи А.Тюрго-Т.Мальтуса гласит: чем выше текущая продуктивность системы П, тем меньше окажется прирост
Пример 3. Всякая система (коллектив, организм, устройство и т.п.) при заданных условиях деятельности имеет определенную продуктивность (производительность) П. Воздействие на систему с целью повышения её продуктивности называется стимуляцией системы. Принцип убывающей отдачи А.Тюрго-Т.Мальтуса гласит: чем выше текущая продуктивность системы П, тем меньше окажется прирост 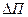 её продуктивности за счет воздействия очередной порции стимулятора. Например, размер оплаты труда стимулирует рост производительности работника П до определенного предела. По мере увеличения зарплаты (интенсивности труда П), стимулирующей эффект
её продуктивности за счет воздействия очередной порции стимулятора. Например, размер оплаты труда стимулирует рост производительности работника П до определенного предела. По мере увеличения зарплаты (интенсивности труда П), стимулирующей эффект 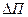 от очередной надбавки к зарплате
от очередной надбавки к зарплате 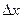 неуклонно снижается.
неуклонно снижается.
| VI Тенденция убывания с монотонно возрастающей скоростью описывается выпуклой убывающей кривой y=f(x),производная которой отрицательна и монотонновозрастает по абсолютной величине. В чистом виде такая тенденция встречается редко. Наблюдается в составных моделях. | у 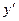 х х х х |
В некоторых экономических процессах с увеличением факторного признака х происходит смена одной тенденции на другую, тогда рассматривают составные модели, включающие в себя несколько тенденций.
Пример 1 В теории управления, теории развития систем и других используются логические модели, графики которых по форме напоминают букву S: 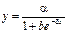 , ( , (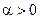 , ,  , , 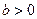 ). Левее точки перегиба кривая описывает тенденцию возрастания с монотонно возрастающей скоростью, ). Левее точки перегиба кривая описывает тенденцию возрастания с монотонно возрастающей скоростью, | 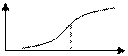 S -образные логические кривые Верхюльста S -образные логические кривые Верхюльста |
справа- тенденцию возрастания с монотонно убывающей скоростью. В точке перегиба происходит смена тенденций.
Пример 2 S -образной кривой описывается зависимость объема производства Q от количества R используемых для этого переменных ресурсов. Слева от точки перегиба доходность возрастает, справа- убывает.
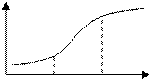 Пример 3 В менеджменте S -образная кривая описывает зависимость между суммарными затратами Х, направленными на развитие технологии и результативностью этих затрат у. При этом крутизна S- образной кривой характеризует эффективность затрат. результативность затрат
Пример 3 В менеджменте S -образная кривая описывает зависимость между суммарными затратами Х, направленными на развитие технологии и результативностью этих затрат у. При этом крутизна S- образной кривой характеризует эффективность затрат. результативность затрат
| Т.о., всякая технология, связанная с производством новых видов изделий или организацией новых форм деятельности, проходит в своем развитии три фазы: 1) фазу зарождения (IФ); 2) фазу быстрого прогресса (IIФ); 3) фазу достижения предела своих потенциальных возможностей (IIIФ). | затраты (IФ) (IIФ) (IIIФ) |
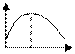
| Пример 4 Функция общей выручки W (x) при определенных условиях деятельности фирмы имеет локальный максимум при х = m. В этой точке тенденция возрастания с монотонно убывающей скоростью сменяется на тенденцию убывания с монотонно возрастающей скоростью. | W (x) m |
 2014-02-09
2014-02-09 1062
1062








