Пусть коммерческая фирма является монополистом, т.е. она единственная торгует на рынке некоторым товаром. Необходимо вырабатывать такую тактику торговли, при которой будет получен максимальный доход П (х), зависящий от объема продаж х, цены товара р (х), издержек от реализации этого товара Z (x).
Пусть р (х) - зависимость цены товара от объема продаж х, тогда общая выручка 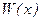 составит
составит
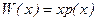 .
.
Доход 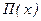 от продажи товара в объеме х представляет разницу между общей выручкой W (х) и издержками Z (x), т.е.
от продажи товара в объеме х представляет разницу между общей выручкой W (х) и издержками Z (x), т.е. 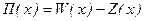 . Т.о., доход
. Т.о., доход 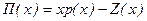 зависит от цены товара и объема х его продаж.
зависит от цены товара и объема х его продаж.
Необходимо выяснить, какова должна быть тактика коммерческой фирмы в отношении цены р (х) и объема продаж х, чтобы получить максимальную выручку W (х), а значит и максимальную прибыль П (х).
Предельной вырцчкой при заданном объеме продаж х называется относительный показатель прироста выручки D W (х) при увеличении объем продаж на величину 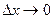 , т.е. величина
, т.е. величина
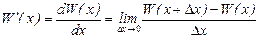 .
.
Предельными издержками называют относительный показатель прироста затрат D Z (х) по реализации товара при увеличении объема продаж с х до х +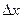 при
при 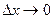
|
|
|
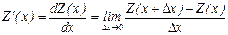 .
.
Если Z (x) = const, т.е. издержки по реализации товара зафиксированы на одном уровне, не зависящем от объема продаж, то предельные издержки равны нулю 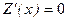 при любом объеме продаж х.
при любом объеме продаж х.
Задача 1 Исследуем на максимум функцию выручки W (x). При объеме продаж 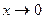 выручка выручка 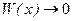 . Если же объем продаж возрастает . Если же объем продаж возрастает 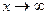 то выручка W (х) может: 1) неограниченно возрастать то выручка W (х) может: 1) неограниченно возрастать 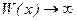 ,
2) асимтиотически стремиться к некоторому пределу ,
2) асимтиотически стремиться к некоторому пределу 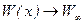 ,
3) сначала увеличивается до некоторого значения W (a), а затем снижаться, т.е. функция W (х) имеет локальный максимум в точке х = а и существует оптимальный объем продаж ,
3) сначала увеличивается до некоторого значения W (a), а затем снижаться, т.е. функция W (х) имеет локальный максимум в точке х = а и существует оптимальный объем продаж 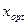 , обеспечивающий максимальное значение выручки max W (x). , обеспечивающий максимальное значение выручки max W (x).
| 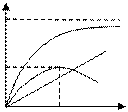 W (x) W (x)
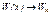
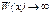 W (а)
а х
W (а)
а х
|
В первом и втором случаях 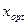 не существует.
не существует.
Пусть W (х) имеет 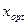 . Найдем
. Найдем 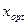 . Функция W (х) достигает своего наибольшего значения в т. экстремума, который возможен в точках, удовлетворяющих условию
. Функция W (х) достигает своего наибольшего значения в т. экстремума, который возможен в точках, удовлетворяющих условию 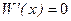 , тогда
, тогда
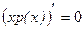 ,
, 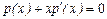 ,
,
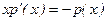 ,
, 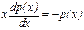 ,
,
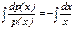 ,
, 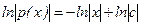 ,
,
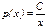 или
или 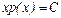 .
.
Пусть 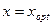 - решение полученного уравнения. В этой точке возможен экстремум функции W (x), который подтвердится при выполнении условия
- решение полученного уравнения. В этой точке возможен экстремум функции W (x), который подтвердится при выполнении условия 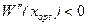 . Тогда
. Тогда 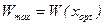 .
.
Задача 2 Исследуем на максимум функцию дохода П (х). Пусть 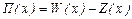 при
при 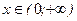 .
.
Деятельность коммерческой фирмы приносит доход П (х) > 0, если W (х) > Z (x), убыточна, если W (х) < Z (x).
Согласно второму достаточному условию существования локального экстримума, функция П (х) имеет локальный максимум при 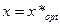 , если выполняются условия
, если выполняются условия 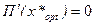 и
и 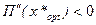 . Для отыскания
. Для отыскания 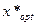 необходимо решить систему
необходимо решить систему 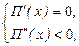 или
или 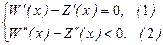
Т.о. для достижения максимального дохода следует установить такую цену р (х) и объем продаж х, чтобы предельные издержки 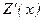 были равны предельной выручке
были равны предельной выручке 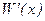 . При этом скорость роста предельной выручки
. При этом скорость роста предельной выручки 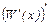 должна быть меньше скорости роста предельных издержек
должна быть меньше скорости роста предельных издержек 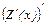 .
.
|
|
|
За.мечание Величины 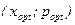 , обеспечивающие максимум функции выручки W (х) не будут совпадать с величинами
, обеспечивающие максимум функции выручки W (х) не будут совпадать с величинами 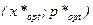 , обеспечивающими максимум функции дохода П (х).
, обеспечивающими максимум функции дохода П (х).
 2014-02-09
2014-02-09 591
591








