2014-02-09
359
Вернемся к задаче, описанной в п. 5.4 формулами (5.22), (5.24), (5.27), (5.26), (5.23). Для определения компромиссного значения цены х объединим задачи (5.22) и (5.26) в задачу максимизации векторного критерия вида
 ,
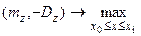| (6.15) |
компоненты которого вычисляются по формулам:
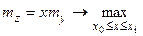; (6.16)
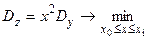. (6.17)
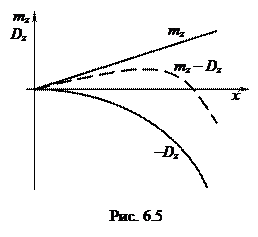
В данной задаче у этих целевых функций отсутствует точка экстремума, однако, их свертка (6.15) имеет ярко выраженный максимум (рис. 6.5).
Отметим, что сформулированная задача относится к классу задач оптимального управления в среднем. В данной работе как развитие рассматривается многокритериальная оптимизация решений в среднем.
Построим линейную свертку критериев:
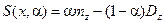, (6.18)
где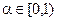 
– параметр свертки.
Паретооптимальные решения задачи (6.18) будем формировать путем решения однокритериальной параметрической задачи оптимизации вида:
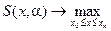. (6.19)
Подставляя в формулу (6.18) выражения (6.16) и (6.17), имеем
 .
|
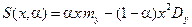Используя необходимые условия экстремума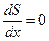 
этой функции, получаем:
 .
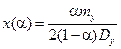| (6.20) |
Значение второй производной
|
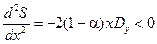
пр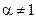и 
и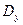 
> 0 говорит о существовании максимума функции (6.18) в точке (6.20).
Удовлетворения ограничения (5.23) при решении задачи (6.15) будем добиваться путем использования в расчетах определенных значений параметра свертки 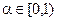. Подставляя выражение (6.20) в неравенство (5.23) и разрешая его относительно a, получаем, что при использовании формулы (5.20) значения параметра a должны принадлежать интервалу 
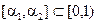, где
 .
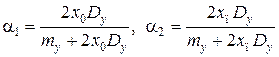| (6.21) |
Построим оптимальные по Парето решения в пространстве критериев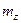 
и 
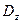. Подставляя (6.20) в выражения (6.16) и (6.17), имеем:
 .
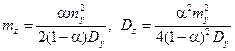| (6.22) |
Исключая из этих выражений параметр a, получаем в пространстве критериев зависимость вида:
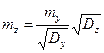, (6.23)
приведенную на рис. 6.6.
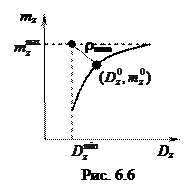Для упрощения процесса принятия решения по цене в паретооптимальном множестве решений в пространстве критериев предлагается построить так называемую «идеальную» точку, не принадлежащую множеству эффективных точек. Координаты «идеальной» точки определяются из выражений
; 
.
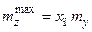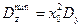Затем найти точку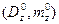 
, наиболее «близкую» к «идеальной» точке 
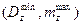, решив задачу
.
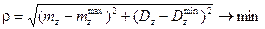Таким образом, формирование паретооптимальных значений розничной цены на рассматриваемый товар осуществляется по следующему алгоритму:
10. По заданным значениям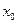 
, 
, 
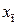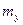и 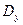по формулам (6.21) вычисляются значения границ интервала 
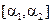варьирования параметра свертки a.
20. Формируется требуемая сетка значений этого параметра
 .
|
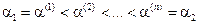30. Для каждого значения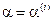 
, 
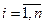по формулам (6.20) и (6.22) вычисляются значения цены 
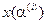, среднего дохода 
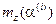и дисперсии дохода 
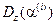, таблица значений которых выдается ЛПР (маркетологу) для принятия решения по конкретному значению розничной цены в ТЦ.
