Наибольшее по модулю собственное значение вещественное, кратное

B этом случае формула (5.3) остается верной, но несколько первых членов можно соединить вместе, так что

y_k=c₁λ₁^k+ c_r+1λ_r+1^k+…+ c_nλ_n^k

где r кратность λ₁.

Все дальнейшие рассуждения остаются в силе и потому

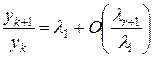. (5.10)

Таким образом, и в этом случае, при условии a ₁≠ 0, отношение y_k-1/y_k дает приближенное значение наибольшего собственного числа.

Вопрос о кратности корня не может быть решен без более детального исследования.

Векторы Y_k=A^kY₀, так же как и в предыдущем случае, сходятся по направлению к одному из собственных векторов, принадлежащих λ₁, именно к собственному вектору, лежащему в циклическом подпространстве, порожденном вектором Y ₀. Исходя из различных начальных векторов, мы придем, вообще говоря, к различным собственным векторам.

Два наибольшие по модулю собственные значения вещественны и противоположны по знаку. Из равенства (5.3) мы видим, что в этом случае четные и нечетные итерации имеют различные коэффициенты при соответствующих степенях λ₁, так как

y_2k=(c₁+c₂)λ₁^2k+c₃λ₃^2k+…+c_nλ_n^2k,

y_2k+1=(c₁-c₂)λ₁^2k+1+c₃λ₃^2k+1+…+c_nλ_n^{2k+ 1},

и поэтому две соседние итерации не могут быть использованы для определения λ₁. Однако, мы можем определить λ₁² по одной из следующих формул:

λ₁²=y_2k+2/y_2k или λ₁²=y_2k+1/y_2k-1. (5.11)

Для нахождения собственных векторов, принадлежащих λ₁ и λ₂ =- λ₁, целесообразно построить векторы Y_k+ λ₁Y_k-1 и Y_k - λ₁Y_k-1. Отношения компонент этих векторов будут стремится, соответственно, к отношению компонент векторов U₁ и U₂, принадлежащих собственным числам λ₁ и λ₂.

Действительно, в силу равенства:

Y_k=a₁λ₁^kU₁+a₂(-λ₁)^kU₂+a₃λ₃^kU₃+ … (5.12)

имеем

Y_k+ λ₁Y_k-1=2 a₁ λ₁^kU₁+ a₃ (λ₃+λ₁) λ₃^k-1 U₃+…=λ₁^k[2a₁U₁+O(λ₃/ λ₁)^k],

Y_k-λ₁Y_k-1=2a₂(-λ₁)^kU₂+a₃(λ₃-λ₁)λ₃^k-1U₃+…=(-λ₁)^k[2a₂U₂+O(λ₃/λ₁)^k]. (5.13)