Нахождение собственных элементов положительно определенной матрицы

Приведем итерационный метод одновременного нахождения собственных значений и собственных векторов положительно определенной матрицы.

Ели действительная матрица

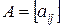
— симметрическая и положительно определенная, то:

1) корни λ₁, λ₂,…, λ_n характеристического уравнения

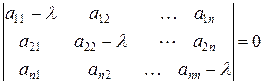(6.1)

действительны и положительны;

2) собственные векторы

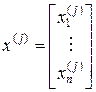, (j=1,2,…,n)

могут быть взяты действительными и удовлетворяют условиям ортогональности

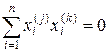при 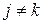. (6.2)

Напишем систему, служащую для определения собственного вектора х⁽¹⁾:

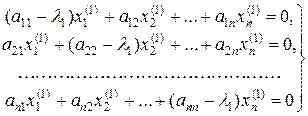
или

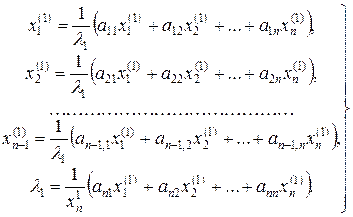(6.3)

Так как координаты собственных векторов определяются с точностью до множителя пропорциональности, то одна из них произвольна, например, за исключением особого случая, можно положить х_n⁽¹⁾ =1. Систему (6.3), вообще говоря, можно решить методом итерации, выбирая подходящие начальные значения x_i^(1,0) и λ₁⁽⁰⁾ и полагая

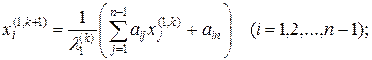
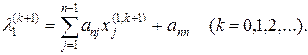
Можно также использовать процесс Зейделя. Таким образом, находятся первый корень характеристического уравнения (6.1)

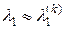(6.4)

и первый собственный вектор

.

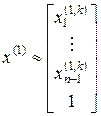Для определения второго корня λ₂ уравнения (6.1) и второго собственного вектора x⁽²⁾ напишем соответствующую систему уравнений

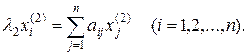(6.5)

Из соотношения ортогональности

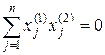(6.6)

исключим одно из неизвестных х_j⁽²⁾, например х_n⁽²⁾. Тогда система (6.5) заменится эквивалентной системой

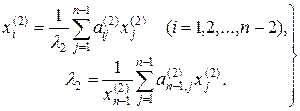(6.7)

Полагая х_n-1⁽²⁾=1, решаем систему (6.7) методом итерации. В результате будут найдены второй корень λ ₂ характеристического уравнения (6.1) и собственный вектор x⁽²⁾, причем n -я координата этого вектора определяется из условия ортогональности (6.6). Аналогично отыскиваются остальные корни λ_j (j = 3,…, п) уравнения (6.1) и соответствующие им собственные векторы х^(j.⁾