Рис. 11
Численное дифференцирование.
При решении практических задач часто нужно найти производные указанных порядков от функции y = f(x), заданной таблично. Возможно также, что в силу сложности аналитического выражения функции f (х) непосредственное дифференцирование ее затруднительно. В этих случаях обычно прибегают к приближенному дифференцированию.
Для вывода формул приближенного дифференцирования заменяют данную функцию f(х) на интересующем отрезке [а, b] интерполирующей функцией Р(х) (чаще всего полиномом), а затем полагают:
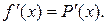
Аналогично поступают при нахождении производных высших порядков функции f (х).
Если для интерполирующей функции Р(х) известна погрешность
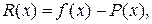
то погрешность производной Р' (х) выражается формулой
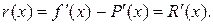
т. е. погрешность производной интерполирующей функции равна производной от погрешности этой функции. То же самое справедливо и для производных высших порядков.
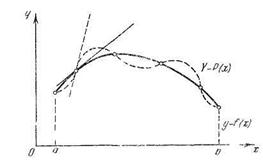
Следует отметить, что, вообще говоря, приближенное дифференцирование представляет собой операцию менее точную, чем интерполирование. Действительно, близость друг к другу ординат двух кривых
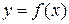 и
и 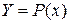
на отрезке [а, b] еще не гарантирует близости на этом отрезке их производных f'(x) и Р' (х), т. е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента (рис. 11).
Пусть имеем функцию y(x), заданную в равноотстоящих точках xi, (i=0,1,2,…,n) отрезка [а, b] с помощью значений 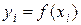 . Для нахождения на [а,b] производных
. Для нахождения на [а,b] производных 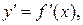
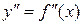 и т.д. функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов x0, x1,…,xk (k≤n).
и т.д. функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов x0, x1,…,xk (k≤n).
Имеем
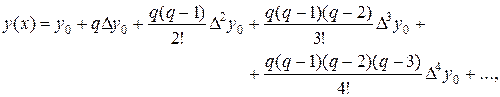 (15.1)
(15.1)
где
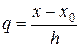 и
и 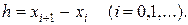
Производя перемножение биномов, получим:
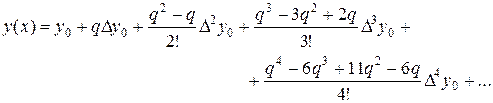 (15.2)
(15.2)
Так как
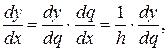
то
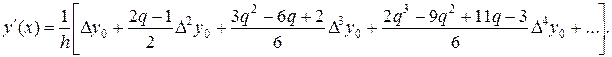 (15.3)
(15.3)
Аналогично, так как
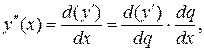
то
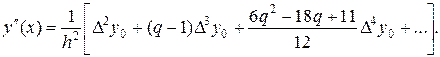 (15.4)
(15.4)
Таким же способом в случае надобности можно вычислить и производные функции у(х) любого порядка.
Заметим, что при нахождении производных у'(х), у"(х),... в фиксированной точке х в качестве х0 следует выбирать ближайшее табличное значение аргумента.
Иногда требуется находить производные функции у в основных табличных точках хi. В этом случае формулы численного дифференцирования упрощаются. Так как каждое табличное значение можно считать за начальное, то положим х = x0, q = 0; тогда будем иметь:
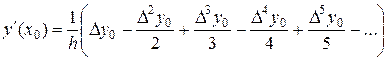 (15.5)
(15.5)
и
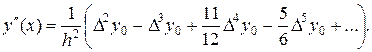 (15.6)
(15.6)
Если 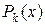 - интерполяционный полином Ньютона, содержащий разности
- интерполяционный полином Ньютона, содержащий разности 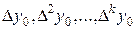 и
и
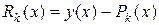
— соответствующая погрешность, то погрешность в определении производной есть
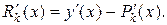
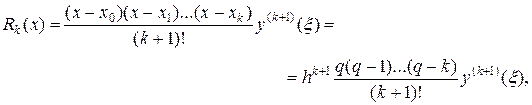
где ξ – некоторое промежуточное число между значениями x0, x1,…,xk, x.
Поэтому, предполагая, что 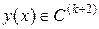 , получим:
, получим:
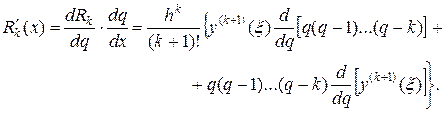
Отсюда при 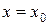 и, следовательно, при q =0 и учитывая, что
и, следовательно, при q =0 и учитывая, что 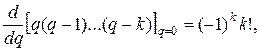 будем иметь:
будем иметь:
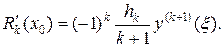 (15.7)
(15.7)
Так как 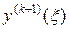 во многих случаях трудно оценить, то при малом h приближенно полагают:
во многих случаях трудно оценить, то при малом h приближенно полагают:
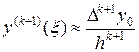
и, следовательно,
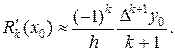 (15.8)
(15.8)
Аналогично может быть найдена погрешность 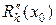 для второй производной
для второй производной 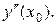
Если функция f (x) непрерывна на отрезке [а, b] и известна ее первообразная F (х), то определенный интеграл от этой функции в пределах от а до b может быть вычислен по формуле Ньютона — Лейбница
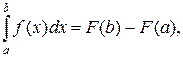 (16.1)
(16.1)
где 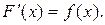
Однако во многих случаях первообразная функция F (х) не может быть найдена с помощью элементарных средств или является слишком сложной; вследствие этого вычисление определенного интеграла по формуле (16.1) может быть затруднительным или даже практически невыполнимым.
Кроме того, на практике подынтегральная функция f (х) часто задается таблично и тогда само понятие первообразной теряет смысл. Аналогичные вопросы возникают при вычислении кратных интегралов. Поэтому важное значение имеют приближенные и в первую очередь численные методы вычисления определенных интегралов.
Задача численного интегрирования функции заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции.
Численное вычисление однократного интеграла называется механической квадратурой, двойного — механической кубатурой. Соответствующие формулы мы будем называть квадратурными и кубатурными формулами.
Остановимся на численном вычислении однократных интегралов. Обычный прием механической квадратуры состоит в том, что данную функцию f(х) на рассматриваемом отрезке [а,b] заменяют интерполирующей или аппроксимирующей функцией φ(x) простого вида (например, полиномом), а затем приближенно полагают:
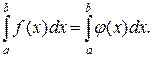 (16.2)
(16.2)
Функция φ(x) должна быть такова, чтобы интеграл 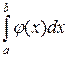 вычислялся непосредственно.
вычислялся непосредственно.
Если функция f(х) задана аналитически, то ставится вопрос об оценке погрешности формулы (16.2).
Рассмотрим более подробно применение для этой цели интерполяционного полинома Лагранжа
Пусть для функции y = f(x) известны в n +1 точках х0, х1, x 2,…, xn отрезка [а,b] соответствующие значения
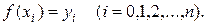 (16.3)
(16.3)
По заданным значениям уi построим полином Лагранжа
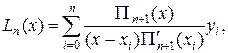 (16.4)
(16.4)
где
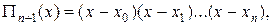
причем
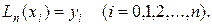
Заменяя функцию f(x) полиномом 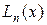 , получим равенство
, получим равенство
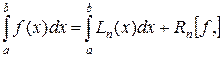 (16.5)
(16.5)
где Rn[f] — ошибка квадратурной формулы (16.5) (остаточный член). Отсюда, воспользовавшись выражением (16.4), получаем приближенную квадратурную формулу
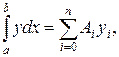 (16.6)
(16.6)
где
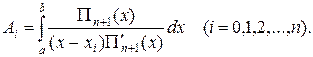 (16.7)
(16.7)
Если пределы интегрирования а и b являются узлами интерполирования, то квадратурная формула (16.6) называется «замкнутого типа», в противном случае — «открытого типа».
Для вычисления коэффициентов Ai заметим, что
1) коэффициенты Ai при данном расположении узлов не зависят от выбора функции f(х);
2) для полинома степени n формула (16.6) – точная, такт как тогда 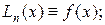 следовательно, в частности, формула (16.6) – точная при k=0,1,…,n.
следовательно, в частности, формула (16.6) – точная при k=0,1,…,n.
Полагая 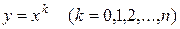 в формуле (16.6), получим линейную систему из n+1 уравнений
в формуле (16.6), получим линейную систему из n+1 уравнений
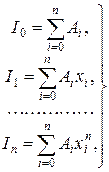 (16.8)
(16.8)
где
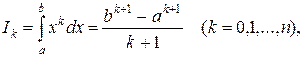
из которой можно определить коэффициенты 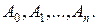
Квадратурные формулы Ньютона — Котеса
Пусть для данной функции у = f (x) требуется вычислить интеграл
Выбрав шаг
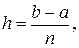
разобьем отрезок [а,b] с помощью равноотстоящих точек
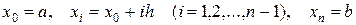
на n равных частей, и пусть
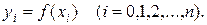
Заменяя функцию у соответствующим интерполяционным полиномом Лагранжа Ln(x), получим приближенную квадратурную формулу
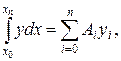 (16.9)
(16.9)
где Ai — некоторые постоянные коэффициенты.
Выведем явные выражения для коэффициентов Ai формулы (16.9). Как известно
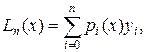 (16.10)
(16.10)
где
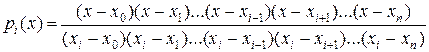 . (16.10)
. (16.10)
Введя обозначения
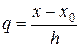 (16.11)
(16.11)
и
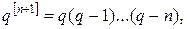 (16.12)
(16.12)
будем иметь
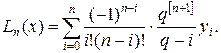 (16.13)
(16.13)
Заменяя в формуле (16.9) функцию y полиномом Ln(x), в силу формулы (16.3) получим:
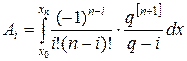
или, так как
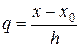 ,
, 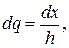
то, сделав замену переменных в определенном интеграле, будем иметь:
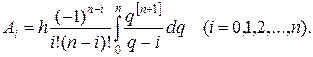
Так как
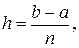
то обычно полагают:
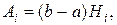
где
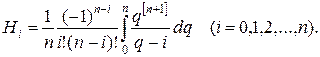 (16.14)
(16.14)
-—постоянные, называемые коэффициентами Котеса.
Квадратурная формула (16.9) при этом принимает вид
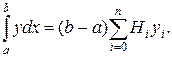 (16.15)
(16.15)
 2014-02-24
2014-02-24 1285
1285
