Приближенное вычисление определенных интегралов по формулам трапеций и Симпсона

Формула трапеций и ее остаточный член. Применяя формулу (16.14), при n = 1 имеем:

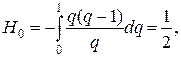
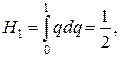
отсюда

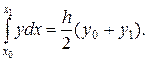(17.1)

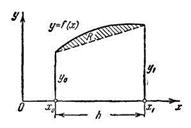
рис. 12

Мы получили известную формулу трапеций для приближенного вычисления определенного интеграла (рис. 12).

Остаточный член (ошибка) квадратурной формулы (17.1) равен

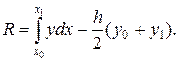
Предполагая, что y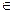C⁽²⁾[a, b], выведем простую формулу для остаточного члена. Будем рассматривать R=R(h) как функцию шага h; тогда можно положить:

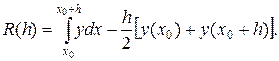
Дифференцируя эту формулу по h последовательно два раза, получим:

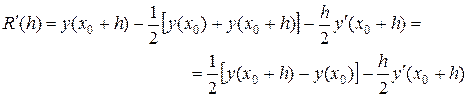
и

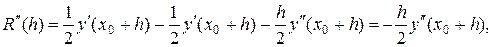
причем

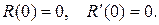
Отсюда, интегрируя по h и используя теорему о среднем, последовательно выводим:

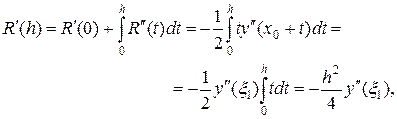
где 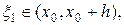и

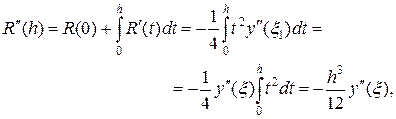
где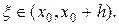

Таким образом, окончательно имеем:

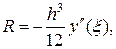(17.2)

где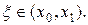

Формула Симпсона и ее остаточный член.

Из формулы (16.14) при п = 2 получаем:

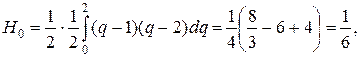
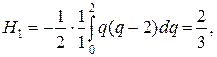
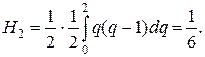
Следовательно,так как х₂- x_o = 2h, имеем:

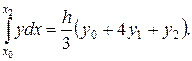(17.3)

Формула (17.3) носит название формулы Симпсона.

Остаточный член формулы Симпсона равен

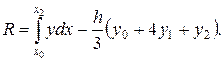
Предполагая, что у 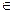С⁽⁴⁾ [а, b], аналогично тому как это делалось для формулы трапеций, выведем более простое выражение для R. Фиксируя среднюю точку х₁ и рассматривая R = R(h) как функцию шага h (h≥0), будем иметь:

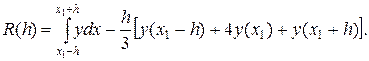
Отсюда, дифференцируя функцию R(h) по h последовательно три раза, получим:

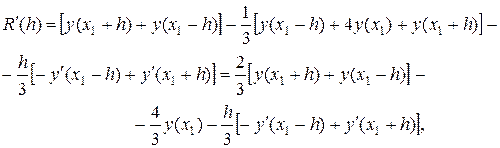
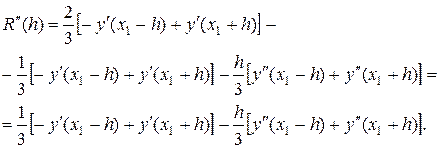
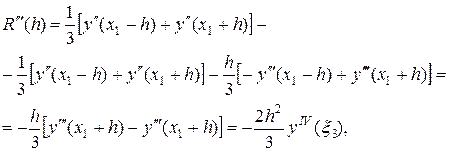
где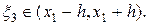

Кроме того, имеем:

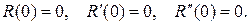
Последовательно интегрируя 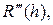используя теорему о среднем, находим:

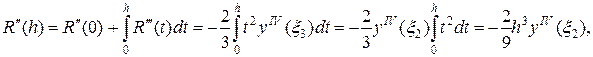
где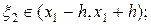

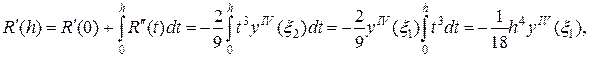
где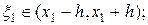

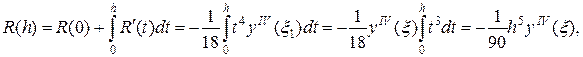
где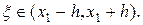

Таким образом, остаточный член формулы Симпсона равен

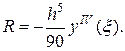(17.4)

Следовательно, эта формула является точной для полиномов не только второй, но и третьей степени, т. е. формула Симпсона при относительно малом числе ординат обладает повышенной точностью.