Оценка погрешности интерполяционной формулы Лагранжа. Для функции y = f(x) мы построили интерполяционный полином Лагранжа Ln(x), принимающий в точках х0, х1,…, хп заданные значения
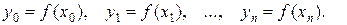
Возникает вопрос, насколько близко построенный полином приближается к функции f(x) в других точках, т. е. как велик остаточный член
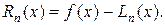
Для определения этой степени приближения наложим на функцию у = f(x) дополнительные ограничения. Именно, мы будем предполагать, что в рассматриваемой области а≤х≤b изменения х, содержащей узлы интерполирования, функция f(x) имеет все производные f '(x), f "(x),…,f(n +1 ) (х) до (п+ 1)-го порядка включительно.
Введем вспомогательную функцию
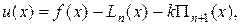 (13.1)
(13.1)
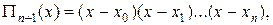
где k — постоянный коэффициент, который будет выбран ниже. Функция и(х), очевидно, имеет п+1 корень в точках 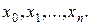
Подберем теперь коэффициент k так, чтобы и(х) имела (n +2)-й корень в любой, нофиксированной точке 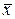 отрезка [a,b], несовпадающей с узлами интерполирования (рис. 10). Для этого достаточно положить
отрезка [a,b], несовпадающей с узлами интерполирования (рис. 10). Для этого достаточно положить
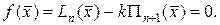
Отсюда, так как 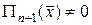 , то
, то
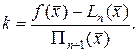 (13.2)
(13.2)
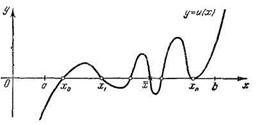
рис. 10
При этом значении множителя k функция u(х) имеет п+2 корня на отрезке [а, b] и будет обращаться в нуль на концах каждого из отрезков
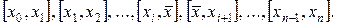
Применяя теорему Ролля к каждому из этих отрезков, убеждаемся, что производная и' (х) имеет не менее п+ 1 корня на отрезке [а, b]. Применив теорему Ролля к производной и'(х), мы убедимся, что вторая производная и" (х) обращается в нуль не менее п раз на отрезке [а, b].
Продолжая эти рассуждения, придем к заключению, что на рассматриваемом отрезке [а, b] производная и(n+1) (х) имеет хотя бы один корень, который обозначим через ξ, т. е, u ( n +1)(ξ)= 0.
Из формулы (13.1), так как
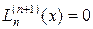 и
и 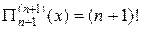 ,
,
имеем:
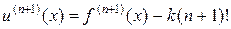
При 
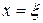 получаем:
получаем:
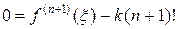
Отсюда
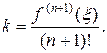 (13.3)
(13.3)
Сравнивая правые части формул (13.2) и (13.3), будем иметь:
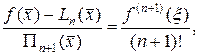
т.е.
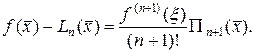 (13.4)
(13.4)
Так как 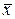 произвольно, то формулу (13.4) можно записать и так:
произвольно, то формулу (13.4) можно записать и так:
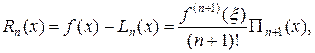 (13.5)
(13.5)
где 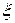 зависит от x и лежит внутри отрезка [а, b].
зависит от x и лежит внутри отрезка [а, b].
Отметим, что формула (13.5) справедлива для всех точек отрезка [а,b], в том числе и для узлов интерполирования.
Обозначая через
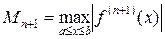 ,
,
мы получаем следующую оценку для абсолютной погрешности интерполяционной формулы Лагранжа:
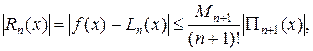 (13.6)
(13.6)
где
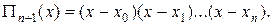 (13.7)
(13.7)
Оценки погрешностей интерполяционных формул Ньютона. Если узлы интерполирования x0, х1,..., хп —равноотстоящие, причем xi+1-xi=h (i = 0, 1, 2,...n —1), то, полагая
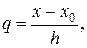
получим остаточный член первой интерполяционной формулы Ньютона
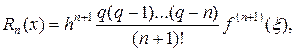 (13.8)
(13.8)
где ξ — некоторое промежуточное значение между узлами интерполирования х0, х1,.... хп и рассматриваемой точкой х. Аналогично, полагая
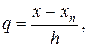
получим остаточный член второй интерполяционной формулы Ньютона
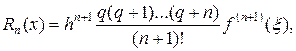
где ξ— некоторое промежуточное значение между узлами интерполирования х0, х1,…,хп и точкой х.
Обычно при практических вычислениях интерполяционная формула Ньютона обрывается на членах, содержащих такие разности, которые в пределах заданной точности можно считать постоянными.
Предполагая, что Δ n+1у почти постоянны для функции y= f(x) и h достаточно мало, и учитывая, что
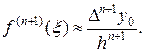
В этом случае остаточный член первой интерполяционной формулы Ньютона приближенно равен
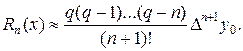
 В этих же условиях для остаточного члена второй интерполяционной формулы Ньютона получаем выражение
В этих же условиях для остаточного члена второй интерполяционной формулы Ньютона получаем выражение
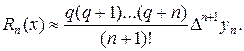
 2014-02-24
2014-02-24 4532
4532
