Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается 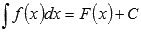 .
.
Выражение 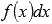 называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
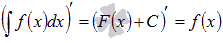
Производная результата интегрирования равна подынтегральной функции.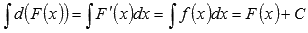
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.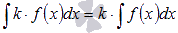 , где k – произвольная константа.
, где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.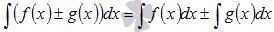
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:
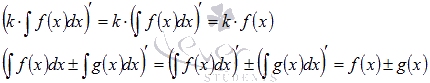
Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
- первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
- второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
· Точно так же из формулы
· 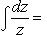
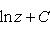
· следует, что
· 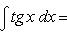
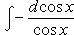
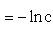
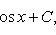
· 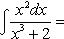
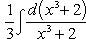
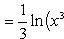
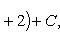
· 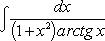
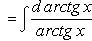
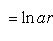
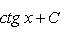
· и т. д.
· Остановимся теперь на другой форме замены переменной. Пусть f (x) - непрерывная функция, заданная на каком-нибудь промежутке [ a, b ]. Допустим, что x = φ (t) есть функция, заданная на другом промежутке [ α, β ], имеющая там производную φ '(t) и удовлетворяющая неравенствам a ≤ φ (t) ≤ b. Пусть, кроме того, существует обратная функция t = ψ (x), заданная на [ a, b ]. Рассмотрим интеграл
· 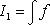
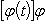
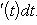
· Согласно сказанному выше для нахождения этого интеграла нужно переписать его в форме
· 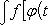
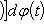
· и заменить φ (t) через x, что приведет нас к интегралу
· 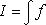
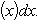
· Этот последний интеграл заведомо существует (т. к. f (x), будучи непрерывной, имеет первообразную). Пусть
· 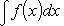
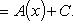
· Тогда, применяя 1-е правило подстановки к интегралу I 1, получим:
· I 1 = A [ φ (t)] + C.
· Пусть A [ φ (t)] = F (t). Заменяя здесь t через ψ (t) и замечая, что φ [ ψ (t)] = x, находим:
· A (x) = F [ ψ (t)].
· Отсюда вытекает, что
· 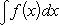
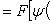
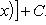
· Если еще заметить, что F (t) есть не что иное, как A [ φ (t)], т. е. первообразная для f [ φ (t)] φ '(t), то сможем формулировать
· Взаимное расположение двух прямых
· Если прямые заданы уравнениями 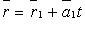 и
и 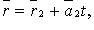 то они:
то они:
· 1) параллельны (но не совпадают) 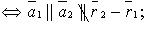
· 2) совпадают 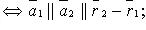
· 3) пересекаются 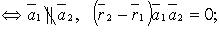
· 4) скрещиваются 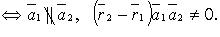
· Если 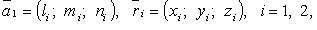 то случаи 1 - 4 имеют место, когда (
то случаи 1 - 4 имеют место, когда (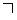 - знак отрицания условия):
- знак отрицания условия):
· 1) 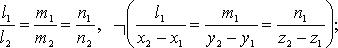
· 2) 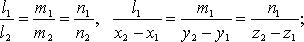
· 3) 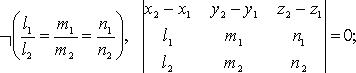
· 4) 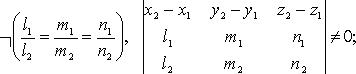
·
Расстояние между двумя параллельными прямыми
· 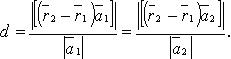
· В координатах
· 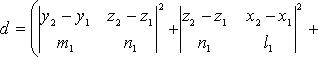
· 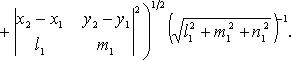
 2014-02-24
2014-02-24 939
939








