Цифровые устройства
Алгебра логики (алгебра Буля)
Цифровые устройства построены на принципе многократного повторения относительно простых базовых схем. Связи между этими схемами строятся на основе чисто формальных методов. Инструментом такого построения служит булева алгебра (алгебра логики).
Логическая переменная Х (или набор переменных – Х1,Х2,….Хn) так же как и функции этой переменной – У, то есть У=f(Х1,Х2,….Хn), принимают только два возможных значения:
- значение логического нуля (низкий уровень (отсутствие) сигнала);
- значение логической единицы (высокий уровень сигнала).
Таким образом алгебра логики изучает связь между переменными, принимающими только значения "1" и "0".
Закон исключенного третьего
Если х ≠ 1, то х = 0, если х ≠ 0, то х = 1.
Существуют три основные операции между логическими переменными:
1) Конъюнкция (операция "и", логическое умножение). Конъюнкция нескольких переменных равна 1 лишь тогда, когда все переменные равны 1. Конъюнкция обозначается в виде произведения у = х1·х2, или у = х1х2, или у = х1Λх2. Обозначение элемента в схеме приведено на рис. 40.
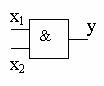
Рис. 40. Конъюнктор
Таблица соответствия для конъюнкции
| х1 | х2 | у=х1·х2 |
Таблица 2 Конъюнкция
2) Дизъюнкция (операция "или", логическое сложение). Дизъюнкция нескольких переменных равна 1, если хотя бы одна из переменных равна 1. Дизъюнкция обозначается в виде суммы: у = х1+х2, или у = х1Vх2. Обозначение элемента в схеме приведено на рис.42.
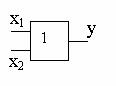
Рис.42. Дизъюнктор
Таблица соответствия для дизъюнкции
| х1 | х2 | у=х1+х2 |
Таблица 3 Дизъюнкция
3) Инверсия (операция "не", логическое отрицание). Обозначение элемента в схеме приведено на рис 43.
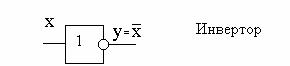
Рис.43
Таблица соответствия для инверсии
| х | у=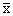
|
Возможны комбинированные операции. Примеры элементов, выполняющих такие действия приведены на рис.44.
Рис. 44 Комбинированные логические элементы
 2014-02-24
2014-02-24 692
692








