Перевод числовой информации из одной позиционной системы в другую

Пример: число 3 5 6 78 заменить равным ему двоичным числом

3 5 6 7
011 101 110 111 3 5 6 7 ₈ = 011 101 110 111₂

Т.е. замена двоичного числа на равное ему восьмеричное может осуществляться механически, без всяких вычислений: машинка с клавишами

0 1 2 3 4 5 6 7

000 001 010 011 100 101 110 111

В процессе преобразования информации в цифровом автомате возникает необходимость перевода чисел из одной позиционной системы счисления в другую. Рассмотрим задачу перевода чисел в общей постановке. Числа в разных системах счисления можно представить следующим образом:

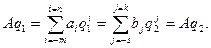(4)

В общем виде задачу перевода числа из системы счисления с основанием q₁ в систему счисления с основанием q₂ можно представить как задачу определения коэффициентов b_i нового ряда, изображающего число в системе с основанием q_2. Решить эту задачу можно подбором коэффициентов b_i. Основная трудность при этом заключается в выборе максимальной степени, которая еще содержится в числе Aq₁. Все действия должны выполняться по правилам q_i – арифметики, т.е. по правилам исходной системы счисления.

После нахождения максимальной степени основания проверяют «вхождение» в заданное число всех степеней нового основания, меньших максимального. Каждая из отмеченных степеней может «входить» в ряд не более q₂ – 1 раз, так как для любого коэффициента ряда накладывается ограничение:

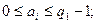
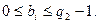
Пример 1. Перевести двоичное число А₂ = 1101001 в десятичную систему счисления (q₂=10).

1⁶1⁵0⁴1³0²0¹1⁰ = 1*2⁶ +1*2⁵ + 0*2⁴ +1*2³ +0*2² +0*2¹ +1*2⁰ = 64+32+8+1=105₁₀

Ответ: А₁₀=105

Пример 2. Перевести двоичное число А₂ = 1100 в десятичную систему счисления (q₂=10)

Переход от одной системы счисления к другой можно продемонстрировать на примере десятичного числа 12, которое в двоичном выражении выглядит так 1100.

1100 = 1*2 ³ + 1*2² + 0*2 ¹ + 0*2 ⁰ = 8+4 = 12 = 1*10¹ + 2*10 ⁰ . Ответ: А₁₀=12

В этом примере числа раскладываются на разряды. Число 1100 состоит из четырех разрядов, которые пронумерованы от нуля до трех, а число 12 – из двух.

Пример 3. Перевести десятичное число А=96 в троичную систему счисления (q₂ = 3).

96 = 0*3⁵ + 1*3⁴ + 0*3³+ 1*3² + 2*3¹ + 0*3⁰ = 10120₃. Ответ: А₃ = 10120.

96: 3 = 32 (остаток 0)

32: 3 = 10 (остаток 2)

10: 3 = 3 (остаток 1)

3: 3 = 1 (остаток 0)

1: 3= 0 (остаток 1)

Рассмотренный в примере прием может использован только при ручном переводе. Для реализации машинных алгоритмов перевода применяют следующие методы.