Основные характеристики ФНЧ

Характеристики в частотной области

Основной параметр АЧХ – частота среза f ср. Это частота, на которой коэффициент передачи K (f) уменьшится на 3 дБ (или в 1.41 раза) по отношению к коэффициенту передачи на нулевой частоте K ₀, .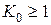

,

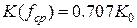Частота подавления 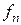- частота, на которой коэффициент передачи фильтра уменьшится до заданной величины .

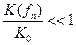Неравномерность АЧХ в полосе пропускания характеризуется коэффициентом допустимых пульсаций

.

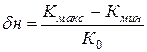При выражении коэффициента передачи децибелах (дБ) для его характеристики в зависимости от частоты используют следующие коэффициенты:

αср - коэффициент характеризующий уменьшение коэффициента передачи по сравнению с K ₀ на 3 дБ на частоте среза;

αп - коэффициент характеризующий уменьшение коэффициента передачи по сравнению с K ₀ на частоте подавления;

α_н – коэффициент характеризующий неравномерность АЧХ в полосе пропускания.

Для измерительных систем используется еще коэффициент

αс - коэффициент характеризующий отклонение коэффициента передачи от K ₀ на максимальной частоте измерительного сигнала, который обрабатывается ФНЧ. Обычно α_с должен иметь достаточно малое значение, например αс 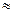0.1 дБ, что эквивалентно спаду K (f _c) относительно К ₀ на ∆ К 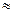0.01 К ₀.

Крутизна спада АЧХ. Она характеризует переходную область от f ср до f подавления и обозначается как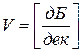

Для фильтра 1-го порядка: .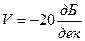

Для фильтра 2-го порядка: ,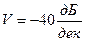

для 3-го порядка: 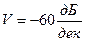и т. д.

Область частот от 0 до f ср – полоса пропускания ФНЧ.

Область частот от f _ср до f _п образует переходную область частот.

Область частот после f _п является областью подавления сигнала.

Групповое время задержки, определяется как производная от фазовой характеристики по частоте

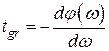. (9.2)

Характеристики во временной области

Для анализа работы ФНЧ во временной области исследуют его переходную характеристику (рисунок 9.3).

Переходной характеристикой h (t) называют реакцию фильтра на единичный скачок напряжения.

Рисунок 9.3 – Переходная характеристика ФНЧ

Параметры, характеризующие ФНЧ во временной области.

1. Время задержки. Измеряется от момента t ₀ до момента достижения выходным сигналом уровня 0.5.

2. Время нарастания или длительность фронта. Отрезок времени между значениями выходного сигнала, составляющими 0.1 и 0.9 от установившегося значения. Для RC цепочки длительность фронта примерно 2.2τ.

3. Время установления. За это время принимаем интервал времени от t ₀ до момента времени, когда сигнал на выходе фильтра войдет в заданную полосу допуска.

4. Коэффициент перерегулирования – превышение выходным сигналом установившегося единичного значения:

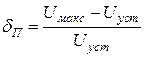. (9.3)

Импульсная переходная характеристика g(t) – это реакция ФНЧ на единичный импульс (δ-функцию). Импульсную переходную характеристику называют еще весовой характеристикой фильтра.

Импульсная переходная характеристика связана с переходной характеристикой соотношением

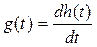. (9.4)

Импульсная переходная характеристика связана с частотной характеристикой преобразованием Фурье:

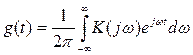. (9.5)

При прямоугольной АЧХ импульсная переходная характеристика имеет вид типа sinx / x (рисунок 9.4)

При реализации фильтров на дискретных элементах обязательно присутствие в фильтре реактивных элементов (С или L). Сколько в схеме реактивных элементов, таким будет и порядок ФНЧ.

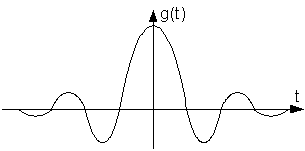
Рисунок 9.4 – Импульсная характеристика ФНЧ с прямоугольной АЧХ

Для общности описания и анализа характеристик фильтров используют переход от текущей частоты к нормированной комплексной переменной

,

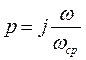где 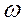- текущая частота,

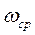- частота среза.

Передаточная функция ФНЧ n -го порядка описывается в общем виде уравнением

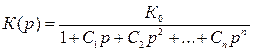, (9.6)

где C ₁, С ₂, …, С _n - положительные действительные коэффициенты.

Для построения реального фильтра необходимо определить корнb полинома n -й степени.

Если корни действительные, то передаточную функцию можно представить в виде:

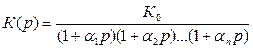, (9.7)

где 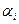- положительные действительные коэффициенты.

Если среди корней полинома есть комплексные, то он раскладывается на произведение сомножителей второго порядка, а передаточная функция ФНЧ представляется в виде

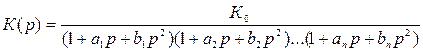, (9.8)

где 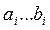- положительные действительные коэффициенты.

Для полиномов нечетной степени 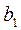=0.

Коэффициенты 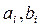определяют характер АЧХ фильтра, т.е. определяют плоскость вершины, крутизну спада АЧХ, и по этим параметрам можно оптимизировать вид АЧХ. Наиболее часто при обработке сигналов применяются следующие фильтры.