10.3.1. Задание: определить сечение трёхгранной призмы (рис. 10.1) плоскостью P(P1P2). Построить полную развёртку поверхности призмы и нанести на ней линию сечения.
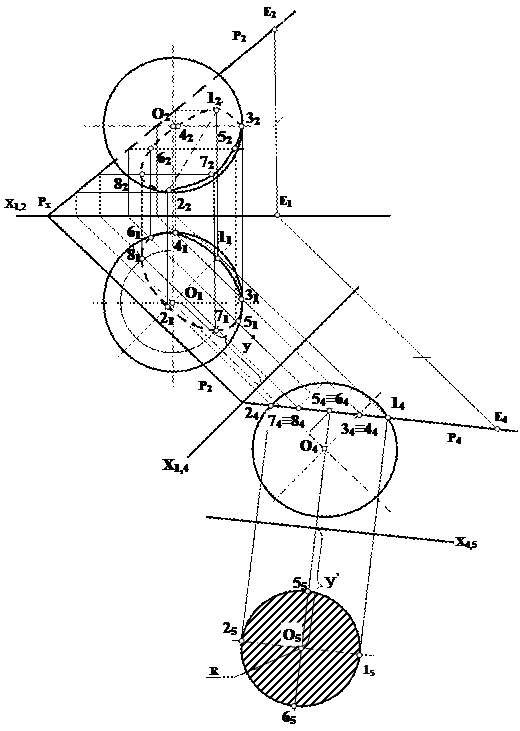
Рис. 11.7
Натуральная величина сечения окружности строится радиусом R, равным половине отрезка 1424.
Поверхность сферы не может быть развёрнута точно. Для неразвертываемых поверхностей строят приближённую развёртку (рис. 11.8).
Поверхность сферы разбивается на равное число частей (рис. 11.8, а), например, на 12 частей. Разбивку производят плоскостями, проходящими через один из диаметров сферы MN.
Каждую часть поверхности сферы, находящуюся между двумя смежными плоскостями, заменяют частью цилиндрической поверхности с осью, проходящей через центр сферы и перпендикулярной к диаметру MN. Диаметр поверхности принимают равным диаметру сферы.
Для наглядности ниже рассмотрено построение только одной из частей поверхности сферы, расположенной между плоскостями Р и Σ.
Выделенную часть поверхности сферы заменяют цилиндрической с осью О1О1, которая перпендикулярна к диаметру MN и плоскости дуги 1-4. Дугу 1-4 делят на равные части (в каждом случае - на три). Для построения развёртки откладывают на вертикальной прямой отрезки, равные хордам данных дуг Δ 1. Величины этих хорд с достаточной степенью точности можно считать равными величинам дуг. По горизонтальной прямой откладывают величины соответствующих образующих поверхности Δ 2, Δ 3 и т.д. Полученные точки соединяют кривой линией (рис. 11.8, б).
 2014-02-24
2014-02-24 824
824








