Вспомогательная секущая плоскость -проецирующая

12.1.1. Задание: определить точки пересечения прямой т с поверхностью пирамиды SABC (рис. 12.1).

Решение: для решения задачи прямую m заключают во фронтально проецирующую плоскость Σ (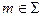).Фронтальная проекция линии пересечения совпадает с фронтальной проекцией следа плоскости Σ ₂. Отмечают проекции точек (1₂, 2₂, 3₂) пересечения плоскостью Σ ребер пирамиды (SA, SB, SC), в которых фронтальный след плоскости Σ пересекает эти ребра. Зная положение линии пересечения (1₂, 2₂, 3₂) на фронтальной проекции, определяют горизонтальную проекцию линии пересечения (1_1,2₁, 3₁). Соединив горизонтальные проекции (1₁,2₁,3₁)точек (1, 2, 3) прямолинейными отрезками ((1₁2₁), (2₁3₁), (З₁1₁)), получают фигуру сечения — треугольник 123. Далее определяют точки пересечения горизонтальной проекции фигуры сечения (1₁2₁3₁) с горизонтальной проекцией m₁ прямой m — точки M₁ и N₁. Затем строят фронтальные проекции (М₂ и N₂) точек пересечения прямой m с поверхностью пирамиды SABC.

Рис.12.1

12.1.2. Задание: определить точки пересечения прямой m с поверхностью прямого кругового цилиндра (рис. 12.2).

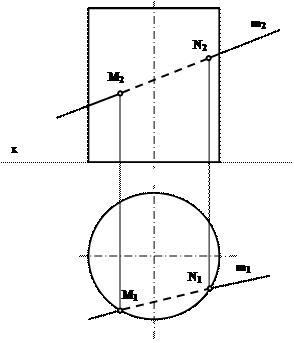Рис.12.2

Решение: при решении задачи выделим проекции то­чек пересечения М и N прямой m с поверхностью цилиндра на горизонтальной проекции - точки m₁ и N₁. Так как образующие прямого кругового цилиндра являются горизонтально проецирующими прямыми, фронтальные проекции точек пересечения прямой т с поверхностью цилиндра М₂ и N₂ находят с помощью линий проекционной связи, как это показано на рисунке.