1) Математическое ожидание
Определение. Математическим ожиданием дискретной случайной величины называется число, равное сумме произведений всех её возможных значений на их вероятности
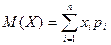 .
.
Вероятностный смысл 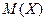 :
: 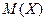 приблизительно равно среднему арифметическому наблюдаемых значений случайной величины.
приблизительно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства 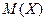
1. 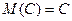 , где С = const;
, где С = const;
2. 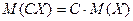 ;
;
3. 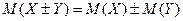 (правило сложенияматематических ожиданий);.
(правило сложенияматематических ожиданий);.
4. 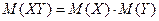 (правило умножения математических ожиданий независимых случайных величин);
(правило умножения математических ожиданий независимых случайных величин);
5. 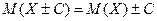 ;
;
6. 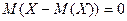 .
.
Пример 4.4. Случайная величина имеет закон распределения

| |||
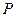
| 0,1 | 0,6 | 0,3 |
Найти ее математическое ожидание.
Решение.
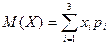 =
=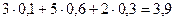 .
.
2) Дисперсия
Дисперсия характеризует разброс значений случайной величины относительно их математического ожидания.
Определение. Дисперсией случайной величины  называется математическое ожидание квадрата её отклонения от математического ожидания
называется математическое ожидание квадрата её отклонения от математического ожидания
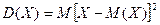 .
.
Получим формулу для вычисления дисперсии:
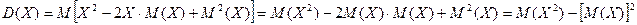
Итак, 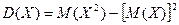 .
.
В качестве показателя рассеивания используют также величину 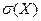 .
.
Определение. Средним квадратическим отклонением 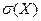 случайной величины называется
случайной величины называется 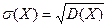 .
.
Свойства 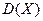
1. 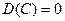 , где С = const;
, где С = const;
2. 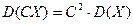 ;
;
3. 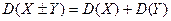 (правило сложения дисперсии независимых случайных величин);
(правило сложения дисперсии независимых случайных величин);
4. 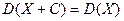 .
.
Пример 4.5. Задана д.с.в.Х. Вычислить ее дисперсию.

| |||
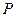
| 0,3 | 0,5 | 0,2 |
Решение. Сначала найдем математическое ожидание этой с.в.
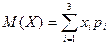 =
=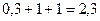 .
.
Составим ряд распределения для с.в. 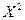 и вычислим ее математическое ожидание:
и вычислим ее математическое ожидание:
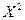
| |||
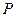
| 0,3 | 0,5 | 0,2 |
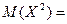
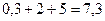 .
.
Используя формулу для расчета дисперсии, получим
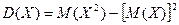 =
=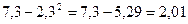 .
.
 2014-02-09
2014-02-09 502
502








