2014-02-09
453
Непрерывную случайную величину можно задать с помощью функции распределения. Так же непрерывную случайную величину можно задавать с помощь другой функции, которая называется плотностью распределения (или плотностью вероятности, или дифференциальной функцией).
Определение. Плотностью распределения непрерывной случайной величины 
называют функцию 
- первую производную от функции распределения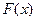 
.
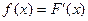Пример 5.1. Задана функция распределения непрерывной случайной величины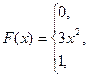 
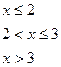. Найти плотность распределения.
Решение. По определению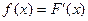 
.
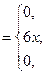
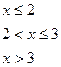Их этого следует, что функция распределения является первообразной для плотности распределения. Зная , можно вычислить вероятность того, что случайная величина примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу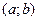 
, равна определенному интегралу от плотности распределения, взятому в пределах от 
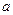до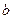 
:
.
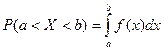Доказательство. Знаем, что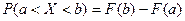 
. По формуле Ньютона-Лейбница 
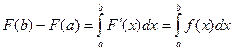. Таким образом, .
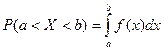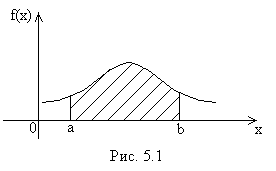
Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу 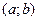, равна площади криволинейной трапеции, ограниченной осью 
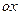, кривой распределения и прямыми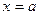 
, 
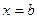(рис. 5.1).
Зная , можно найти функцию распределения 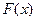по формуле:
.
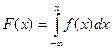График плотности распределения называется кривой распределения.
