Определение. Дискретная случайная величина имеет биноминальный закон распределения, если она принимает значения 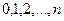 с вероятностями
с вероятностями 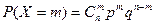 , то есть вероятности находятся по формуле Бернулли, где
, то есть вероятности находятся по формуле Бернулли, где 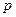 и
и 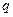 - вероятности появления и непоявления события в каждом испытании.
- вероятности появления и непоявления события в каждом испытании.
Математическое ожидание случайной величины, распределенной по биноминальному закону, то есть 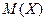 числа появлений события
числа появлений события  в
в  независимых испытаниях, равно произведению числа испытаний на вероятность появления события в каждом испытании:
независимых испытаниях, равно произведению числа испытаний на вероятность появления события в каждом испытании:
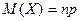 .
.
Дисперсия числа появлений события  в
в  независимых испытаниях равна произведению числа испытаний на вероятности появления и не появления события в одном испытании:
независимых испытаниях равна произведению числа испытаний на вероятности появления и не появления события в одном испытании:
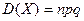 .
.
Пример 4.6. Вероятность попадания в цель при стрельбе из орудия 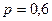 . Составить ряд распределения числа попаданий, если произведено 3 выстрела. Найти
. Составить ряд распределения числа попаданий, если произведено 3 выстрела. Найти 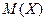 и
и 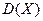 .
.
Решение. Вероятность попадания в цель равна 0,6. Тогда вероятность промаха 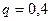 . Случайная величина Х – число попаданий принимает четыре значения: 0,1,2,3.
. Случайная величина Х – число попаданий принимает четыре значения: 0,1,2,3.
Найдем вероятности этих значений.
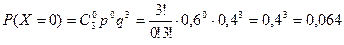 ;
;
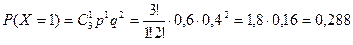 ;
;
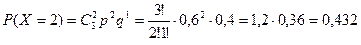 ;
;
 | ||||
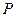 | 0,064 | 0,288 | 0,432 | 0,216 |
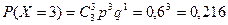 .
.
Итак, ряд распределения имеет вид
Контроль: 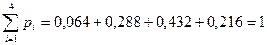 .
.
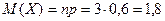 .
.
 .
.
Определение. Дискретная случайная величина  имеет закон распределения Пуассона, если она принимает значения
имеет закон распределения Пуассона, если она принимает значения 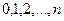 с вероятностями
с вероятностями 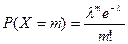 , где
, где 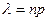 .
.
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру 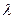 этого закона:
этого закона:
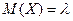 ,
, 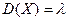 .
.
 2014-02-09
2014-02-09 2549
2549
