Тема 5. Непрерывные случайные величины

Свойства функции распределения

1. ;

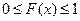2. ,

;

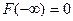3. .

4. 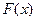- неубывающая функция.

Пример 4.8. Функция распределения с.в.имеет вид .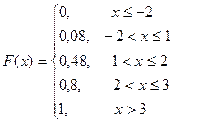

Найти вероятность того, что случайная величина примет значение в интервале .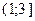

Решение.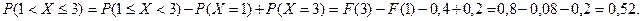

Нормальный закон распределения

Определение. Случайная величина называется непрерывной, если её функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.

Доказательство. Представим следующим образом

.

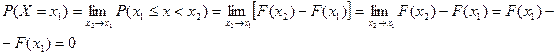Следствие. Если - непрерывная случайная величина, то вероятность попадания случайной величины в интервал 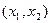не зависит от того, является этот интервал открытым или закрытым, то есть

.