Пусть д.с.в. Х задана в виде ряда распределения
| Х | х 1 | х 2 | … | х n |
| Р | p1 | p2 | … | pn |
1) Произведением случайной величины  на постоянную величину
на постоянную величину 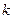 называется случайная величина
называется случайная величина 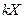 , которая принимает значения
, которая принимает значения 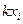 с теми же вероятностями
с теми же вероятностями 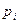 .
.
2) m - й степенью случайной величины  , то есть
, то есть 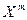 называется случайная величина, которая принимает значения
называется случайная величина, которая принимает значения 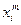 с теми же вероятностями
с теми же вероятностями 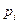 .
.
Пример 4.2. Задана случайная величина Х
 | -2 | ||
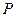 | 0,5 | 0,2 | 0,3 |
Найти закон распределения случайных величин а) 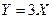 , б)
, б) 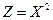 .
.
Решение.
а) Возможные значения с.в. таковы:
таковы: 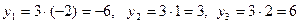 .
.
Вероятности этих значений равны вероятностям соответствующих значений с.в. Х.
 | -6 | ||
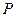 | 0,5 | 0,2 | 0,3 |
б) Возможные значения с.в. Z таковы: 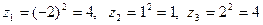 .
.
При этом 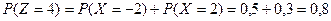 .
.
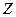 | ||
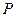 | 0,2 | 0,8 |
Таким образом
3) Суммой (разностью или произведением) случайных величин  и
и  называется случайная величина, которая принимает все возможные значения вида
называется случайная величина, которая принимает все возможные значения вида 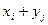 (
(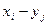 ,
,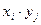 ) с вероятностями
) с вероятностями 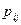 того, что случайная величина
того, что случайная величина  примет значение
примет значение 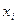 , а
, а  - значение
- значение 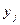 :
:
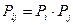 ,
,
где 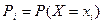 ,
, 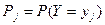 .
.
Пример 4.3. Заданы законы распределения случайных величин  и
и  :
:
 | ||
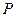 | 0,2 | 0,8 |
 | -1 | ||
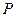 | 0,3 | 0,5 | 0,2 |
Найти закон распределения с.в.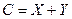 .
.
Решение. Найдем возможные значения с.в. С:
-1 = 0 + (-1); 0 = 0 + 0; 1 = 0 + 1; 0 = 1 + (-1); 1 = 1 + 0; 2 = 1 + 1, т.е.
с.в. С принимает значения: 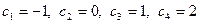 .
.
Находим вероятности этих значений:
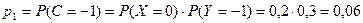 ,
,
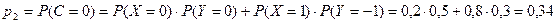 ,
,
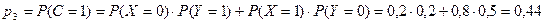 ,
,
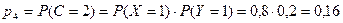 .
.
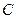 | -1 | |||
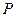 | 0,06 | 0,34 | 0,44 | 0,16 |
 2014-02-09
2014-02-09 2613
2613








