2014-02-09
449
Определение. Интервальной называют оценку, которая определяется двумя числами – концами интервала.
Интервальные оценки позволяют установить точность и надёжность оценок. Пусть найденная по результатам выборки статистическая характеристика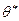 
служит оценкой неизвестного параметра 
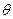. Ясно, что чем меньше 
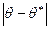, тем точнее оценка. Другими словами, если 
(
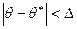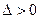), то чем меньше 
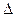, тем оценка точнее. Таким образом 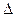характеризует точность оценки. Однако, мы не можем категорически утверждать, что оценка 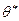удовлетворяет неравенству 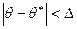. Мы можем лишь говорить о вероятности 
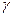, с которой это неравенство осуществляется.
Определение. Надёжностью (доверительной вероятностью) оценки параметра 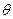по 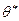называется вероятность 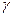, с которой осуществляется неравенство .
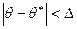Обычно надёжность задаётся наперед, причём чаще всего близка к единице.
Например, =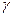
.
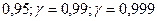Пусть вероятность того, что 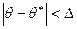равна :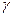
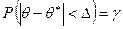или
.
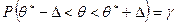Данное соотношение понимают так: вероятность того, что интервал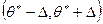 
заключает в себе (покрывает) неизвестный параметр 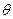, равна .
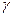Интервал 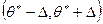называется доверительным.
Величина доверительного интервала существенно зависит от объёма выборки 
(уменьшается с ростом ) и от значения доверительной вероятности 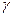(увеличивается с приближением 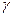к единице).
Определение. Наибольшее отклонение 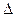выборочной средней (или выборочной доли) от генеральной средней (или генеральной доли), которое возможно с заданной доверительной вероятностью 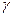, называется предельной ошибкой выборки (точность оценки).
Эту ошибку называют случайной ошибкой репрезентативности. Систематическая ошибка репрезентативности появляется в результате нарушения принципа случайности при отборе элементов в выборку.
