Основные свойства дисперсии

1) Дисперсия постоянной равна нулю.

2) Если все варианты увеличить (уменьшить) в 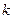раз, то дисперсия увеличится (уменьшится) в 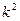раз

.

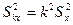3) Если все варианты увеличить (уменьшить) на одно и то же число, то дисперсия не изменится

.

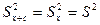4) Дисперсия равна разности между средней арифметической квадратов вариант и квадратом средней арифметической

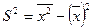- формула для расчета дисперсии.

Пример 8.2. Вычислить 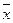, 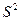распределения, заданного таблицей:

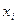Решение.

.

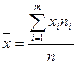
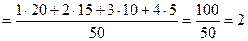
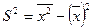
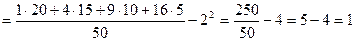Упрощённый способ расчёта средней арифметической и дисперсии

Вычисление средней арифметической вариационного ряда можно упростить, если использовать не первоначальные варианты 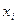, а новые варианты – условные варианты ,

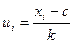где 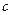и 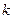- специально подобранные постоянные.

В качестве с рекомендуется брать варианту, которая расположена примерно в середине вариационного ряда. В качестве 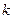необходимо взять величину интервала по 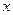. Тогда

, .

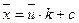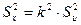Определение. Медианой Ме вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений.

Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному интервалу, а для ряда с четным числом членов – полусумме двух серединных вариантов.

Определение. Модой Мо вариационного ряда называется вариант, которому соответствует наибольшая частота.