10.1. Статистическая гипотеза и общая схема её проверки
Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определённый вид, то выдвигают гипотезу: генеральная совокупность распределена по закону  . Или, если закон распределения известен, а его параметры неизвестны, тогда выдвигают гипотезу: неизвестный параметр
. Или, если закон распределения известен, а его параметры неизвестны, тогда выдвигают гипотезу: неизвестный параметр 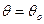 .
.
Определение. Статистической гипотезой называется предположение о виде неизвестного распределения, или о параметрах известного распределения.
Кроме выдвинутой гипотезы рассматривают и противоречащую ей гипотезу.
Определение. Нулевой (основной) называют выдвинутую гипотезу 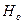 . Конкурирующей (альтернативной) называют гипотезу
. Конкурирующей (альтернативной) называют гипотезу 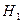 , которая противоречит нулевой.
, которая противоречит нулевой.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость её проверки. В результате проверки гипотезы может быть принято неправильное решение, то есть могут быть допущены ошибки:
ошибка I-го рода состоит в том, что будет отвергнута правильная гипотеза;
ошибка II-го рода состоит в том, что будет принята неправильная гипотеза.
Определение. Вероятность совершить ошибку I-го ряда принято обозначать через 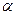 - её называют уровнем значимости.
- её называют уровнем значимости.
Наиболее часто уровень значимости принимают равным 0,05 или 0,01.
Например, если 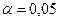 - это значит, что в пяти случаях из 100 имеет риск допустить ошибку I-го рода (отвергнуть правильную гипотезу).
- это значит, что в пяти случаях из 100 имеет риск допустить ошибку I-го рода (отвергнуть правильную гипотезу).
Вероятность допустить ошибку II-го рода – обычно обозначают 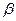 .
.
Определение. Вероятность 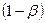 не допустить ошибку II-го рода, то есть отвергнуть гипотезу
не допустить ошибку II-го рода, то есть отвергнуть гипотезу 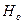 , когда она неверна, называется мощностью критерия.
, когда она неверна, называется мощностью критерия.
Например, с точки зрения юриста: 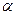 - вероятность вынесения судом обвинительного приговора, когда на самом деле объявляемый невиновен,
- вероятность вынесения судом обвинительного приговора, когда на самом деле объявляемый невиновен, 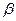 - вероятность вынесения судом оправдательного приговора, когда на самом деле обвиняемый виновен в совершении преступления.
- вероятность вынесения судом оправдательного приговора, когда на самом деле обвиняемый виновен в совершении преступления.
Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно.
Определение. Статистическим критерием называют случайную величину 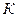 , которая служит для проверки нулевой гипотезы.
, которая служит для проверки нулевой гипотезы.
Определение. Наблюдаемым критерием 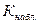 называют значение критерия, вычисленное по выборке.
называют значение критерия, вычисленное по выборке.
После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – при которых она принимается.
Определение. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Определение. Областью принятия гипотезы называют совокупность значений критерия, при которых гипотезу принимают.
Определение. Критическими точками 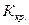 называют точки, отделяющие критическую область от области принятия гипотезы.
называют точки, отделяющие критическую область от области принятия гипотезы.
Определение. Правосторонней (левосторонней) критической областью называют критическую область определяемую неравенством 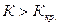
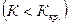 , где
, где 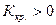
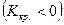 .
.
Основные принципы проверки статистических гипотез: если 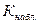 принадлежит критической области, то гипотезу отвергают, если
принадлежит критической области, то гипотезу отвергают, если 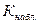 принадлежит области принятия гипотезы, то гипотезу принимают.
принадлежит области принятия гипотезы, то гипотезу принимают.
Для того чтобы найти критическую область, необходимо найти критическую точку. Для этого задают достаточно малую вероятность – называемую уровнем значимости 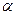 и задают следующие условия:
и задают следующие условия:
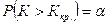 - для правосторонней области,
- для правосторонней области,
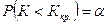 - для левосторонней области.
- для левосторонней области.
Для каждого критерия существуют таблицы, по которым и находят критическую точку 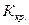 . Когда
. Когда 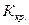 найдено, то по данным выборки вычисляют
найдено, то по данным выборки вычисляют 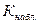 . Для правосторонней критической области если
. Для правосторонней критической области если
1) 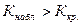 - то нулевую гипотезу
- то нулевую гипотезу 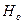 отвергают,
отвергают,
2) 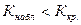 - то нет оснований отвергнуть
- то нет оснований отвергнуть 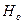 .
.
 2014-02-09
2014-02-09 2022
2022
