Пусть необходимо определить вид и параметры закона распределения некоторой случайной величины. Параметры распределения, как правило, не известны, поэтому их заменяем наилучшими оценками по выборке. Как бы хорошо не был подобран закон распределения, между эмпирическим и теоретическим распределениями неизбежны расхождения. Необходимо ответить на вопрос: эти расхождения являются случайными, связанными с ограниченным числом наблюдений, или они связаны с тем, что теоретический закон распределения подобран неудачно. Для ответа служат критерии согласия.
Определение. Критерий согласия – это некоторая случайная величина, характеризующая степень расхождения теоретического и эмпирического распределений.
Имеется несколько критериев согласия. Мы рассмотрим критерий согласия Пирсона 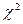 (хи-квадрат). Данный критерий основан на сравнении эмпирических частот и теоретических частот.
(хи-квадрат). Данный критерий основан на сравнении эмпирических частот и теоретических частот.
Определение. Теоретическими частотами называют частоты 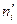 , найденные в отличие от фактически наблюдаемых частот
, найденные в отличие от фактически наблюдаемых частот 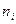 теоретически и равные
теоретически и равные
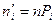 ,
,
где  - число испытаний,
- число испытаний, 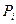 - вероятность попадания с.в.
- вероятность попадания с.в. в
в 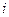 - й частичный интервал, вычисленная при условии, что с.в.
- й частичный интервал, вычисленная при условии, что с.в. имеет определенное распределение.
имеет определенное распределение.
Если предполагаем, что с.в. распределена нормально, то
распределена нормально, то
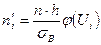 ,
,
где  - объём выборки;
- объём выборки; 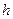 - длина частичного интервала;
- длина частичного интервала; 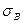 - выборочное среднеквадратическое отклонение;
- выборочное среднеквадратическое отклонение;  , где
, где 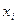 - середина i-го частичного интервала,
- середина i-го частичного интервала, 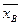 - выборочная средняя,
- выборочная средняя, 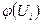 - затабулированная функция.
- затабулированная функция.
Итак, пусть по выборке объёма  получено эмпирическое распределение
получено эмпирическое распределение
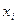 | 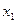 | 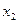 | 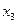 | … | 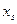 |
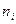 | 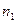 | 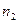 | 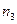 | … | 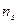 |
Допустим, что вычислены теоретические частоты 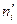
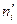 | 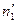 | 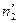 | 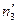 | … | 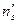 |
При уровне значимости 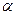 проверяем нулевую гипотезу
проверяем нулевую гипотезу 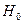 - генеральная совокупность распределена по нормальному закону. В качестве критерия проверки гипотезы
- генеральная совокупность распределена по нормальному закону. В качестве критерия проверки гипотезы 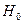 применим случайную величину
применим случайную величину 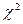 , равную сумме квадратов отклонений эмпирических частот от теоретических:
, равную сумме квадратов отклонений эмпирических частот от теоретических:
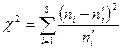 . (10.1)
. (10.1)
Доказано, что при 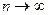 закон распределения случайной величины (10.1), независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения
закон распределения случайной величины (10.1), независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения 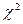 с
с 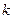 степенями свободы. Поэтому случайная величина (10.1) и обозначена через
степенями свободы. Поэтому случайная величина (10.1) и обозначена через 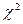 , а сам критерий называется критерием согласия
, а сам критерий называется критерием согласия 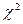 .
.
где 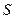 - число частичных интервалов выборки,
- число частичных интервалов выборки, 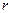 - число параметров предполагаемого распределения. В случае нормального распределения
- число параметров предполагаемого распределения. В случае нормального распределения 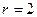 (
(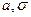 ).
).
Т.о. для нормального распределения 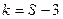 .
.
 2014-02-09
2014-02-09 1716
1716

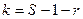 ,
,