2014-02-09
361
Это отношение преобразования Лапласа к рассматриваемому воздействию, а все остальные внешние воздействия равняются нулю. Вычисления производятся при нулевых начальных условиях.
W(z) =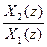 
- по входному воздействию;
Wf(z) =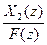 
- по возмущению;
X2 (z) = L { x2 (t)} =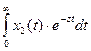 
X1 (z) = L { x1 (t)} =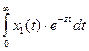 
преобразования Лапласа (или “изображения”)
F (z) = L { f (t)} =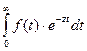 
x2 (t), x1, (t), f (t) – называются оригиналами.
x2 (0) =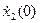
=…= x2(n) (0) = 0
нулевые начальные условия
x1 (0) =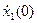
=…= x1(m) (0) = 0
W(z) – основная передаточная функция
f (0) =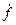 
(0) = …= f(q) (0) = 0 Wf(z) – передаточная функция
Операционный метод и его приложения в теории автоматического регулирования.
Требуется найти х (t).
Введем оператор р = s –i·s, где i =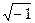 
1) Функция вещественной переменной х (t), переходим в плоскость комплексной
переменной Х(р)
2) операторное уравнение
3) разрешаем операторное уравнение относительно Х(р)
4) переходим в вещественную плоскость х (t) (оригинал)
Преобразования Лапласа
Определение
Функция- оригинал, это функция f(t), которая удовлетворяет условию:
1) f(t) непрерывна вместе с производными высокого порядка вдоль всей оси, но допускается конечно число разрывов I рода.
2) для всех t < 0, f(t) = 0
3) f(t)возрастает не быстрее некоторого показателя функции: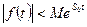 
,
M > 0, S0 > 0 – показатель роста
Пример:
