F(x2(n),x2(n-1), …, 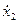 , x2; x1(m), …,
, x2; x1(m), …,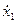 ,x1; f(q), …,
,x1; f(q), …,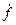 , f) = 0
, f) = 0
Если эта функция – нелинейная, она описывается нелинейными дифференциальными уравнениями, и звено – нелинейное.
Если уравнение линейное – звено нелинейное.
Производим линеаризацию нелинейного уравнения, т.е. разложим функцию в ряд Тейлора.
Линеаризация производится относительно некоторого режима.
Режим должен быть установившимся, т.е. x1 = x10; x2 = x20; f1 = f10 - постоянные величины, следовательно их производные равны 0: F(0, x20; 0, x10;0, f10)
Пусть F(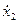 , x2;,x1; f) = 0 (**)
, x2;,x1; f) = 0 (**)
1. Все координаты рассматриваются как x1 = x10 + ∆ x1; x2 = x20 + ∆ x2; f = f10 + ∆ f1
2. Левая часть уравнения раскладывается в ряд Тейлора:
F( 0, x20; x10;, f10) + 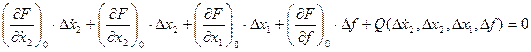
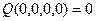
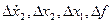 - малые отклонения
- малые отклонения
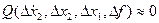
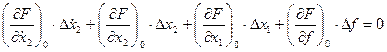 - линейное дифференциальное уравнение с постоянными коэффициентами – результат линеаризации.
- линейное дифференциальное уравнение с постоянными коэффициентами – результат линеаризации.
 x1 = x10;
x1 = x10;
x2 = x20;
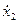 =
= 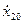 ; - координаты точки, относительно которой идет расположение
; - координаты точки, относительно которой идет расположение
f1 = f10
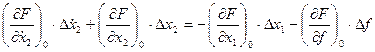
Обозначим: Со = 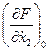 ; С1 =
; С1 = 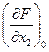 ; Bo = -
; Bo = - 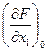 ; ro = -
; ro = -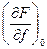
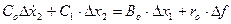
Вводим символический оператор дифференцирования:
р = 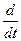 (…); рxk =
(…); рxk = 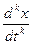 (…);
(…); 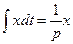 , k = 1,2,…
, k = 1,2,…
(Co·p + C1)· ∆ x2 = Bo·∆ x1 + ro·∆ f
 Обозначим: С(р) = Со·р + C1
Обозначим: С(р) = Со·р + C1
B(p) = Bo
r(p) = ro
Получим уравнение 1-го порядка: С(р)· ∆ x2 = B(p) ·∆ x1 + r(p) ·∆ f
(Co·p + C1)· ∆ x2 = Bo·∆ x1 + ro·∆ f; пусть С1 ≠ 0, тогда введем Т = 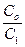 ; К =
; К = 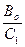 ; Кf =
; Кf = 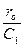 ;
;
Тогда получим: (T·p + 1)· ∆ x2 = K·∆ x1 + Kf··∆f
[ p ] = 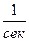 ; [ T ] = сек; [ К ] =
; [ T ] = сек; [ К ] = 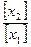 ; [ Кf ] =
; [ Кf ] = 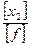 ;
;
T – постоянная времени;
K – коэффициент по входной величине;
Kf – коэффициент по возмущению.
Линеаризируем F(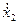 ,
,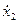 , x2;
, x2; 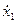 ,x1;
,x1;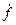 ,f) = 0
,f) = 0
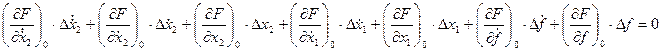
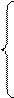
С(р) = Со·р2 + С1·р+ C2;
B(p) = Bo·р + B1 ;
r(p) = ro·р + r1;
где Со = 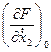 ; С1 =
; С1 = 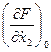 ; С2 =
; С2 = 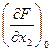 ; Bo = -
; Bo = - 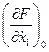 ;
;
B1 = - 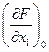 ; ro = -
; ro = -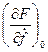 ; r1 = -
; r1 = -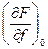
 2014-02-09
2014-02-09 723
723








