Сопряженные операторы

Лекция 6 Сопряженные операторы. Примеры сопряженных операторов

6.1. Сопряженные операторы

6.2. Примеры сопряженных операторов

Пусть X и Y – банаховы пространства, A : X ® Y – ограниченный линейный оператор. Возьмем функционал f Î Y' и по нему построим новый функционал g (x) = f (Ax). Проверим, что g – линейный ограниченный функционал на X. Равенства

g (x ₁ + x ₂) = f (A (x ₁ + x ₂) ) = f (Ax ₁) + f (Ax ₂) = g (x ₁) + g (x ₂),

g (l x) = f (A (l x) ) = l f (Ax) = l g (x)

вытекают из линейности функционала f и оператора A. Из неравенства

| g (x) | = | f (Ax) | £ || f || || Ax || £ || f || || A || || x ||

получаем, что g – ограниченный линейный функционал и что

|| g || £ || A || || f ||. (1)

Таким образом, возникает отображение

A' : Y' ' f ® g Î X'.

Определение 6.1. Сопряженным оператором к линейному ограниченному оператору A : X ® Y называется оператор A', действующий по формуле A' f (x) = f (Ax) из пространства Y' в пространство X'.

Замечание 6.1. В выражении A' f (x) из двух возможных вариантов расположения скобок (A' f )(x) и A' ( f (x) ) второй не имеет смысла ( f (x) – число и оператор A' нельзя применить к числу), поэтому выраженне A' f (x) читается по первому варианту (оператор A' применяется к функционалу f и вычисляется значение нового функционала в точке x).

Покажем, что операция сопряжения не выводит из класса ограниченных линейных операторов.

Теорема 6.1. Оператор A', сопряженный к линейному ограниченному оператору A, является линейным ограниченным, причем || A' || = || A ||.

Доказательство. Проверим линейность оператора A':

A' ( f ₁ + f ₂ )(x) = ( f ₁ + f ₂ )(Ax) = f ₁(Ax) + f ₂(Ax) = A' f ₁(x) + A' f ₂(x),

A' (l f )(x) = l f (Ax) = l A' f (x).

Согласно неравенству (1), получаем неравенство

|| A' f || = || g || £ || A || || f ||,

т. е. оператор A' ограничен и || A' || £ || A ||. Покажем, что справедливо обратное неравенство || A || £ || A' ||. Возьмем произвольный элемент x Î X и пусть y = A x. Согласно следствию 4.2 теоремы Хана – Банаха, существует такой функционал f Î Y', что || f || = 1 и f (y) = || y ||. Тогда f (Ax) = || Ax || и

|| Ax || = | f (Ax) | = | A' f (x) | £ || A' || || f || || x || £ || A' || || x ||.

Таким образом, для любого x Î X выполнено || Ax || £ || A' || || x ||, откуда получаем || A || £ || A' || и, значит, || A' || = || A ||. Теорема доказана.

Замечание 6.2. Из равенства A' f (x ₁ + x ₂) = A' f (x ₁) + A' f (x ₂) следует аддитивность функционала A' f, но не оператора A'.

Построив для каждого оператора A его сопряженный A', мы определили отображение, действующее из L (X, Y) в L (Y', X'), которое оператору A ставит в соответствие его сопряженный A'. Это отображение называют отображением сопряжения. Отметим следующие свойства сопряжения: 1) (A + B) ' = A' + B', 2) (l A) ' = l A' (линейность); 3) || A' || = || A || (изометричность).

Если X = Y, то дополнительно отметим: 4) I'_X = I_{X '}; 5) (A B) ' = B'A'.

Докажем равенство 5) (заметим, что в правой части сомножители берутся в обратном порядке). Имеем (A B) ' f (x) = f (A B x), A' f (x) = f (A x) = g (x),
B'A' f (x) = g (B x) = f (A B x), т. е. (A B) ' = B'A'.

6) Если оператор A имеет ограниченный обратный A ^{– 1}, то A' также обратим и (A' ) ^{– 1} = (A ^{– 1} ) '.

Доказательство. Так как A A ^{– 1} = I и A ^{– 1} A = I, то, согласно свойствам 4) и 5), будем иметь (A ^{– 1} ) 'A' = I и A' (A ^{– 1} ) ' = I, т. е. оператор (A ^{– 1} ) ' является обратным к оператору A'. Свойство доказано.

Приведем несколько задач, при решении которых естественно возникают сопряженные операторы.

Пусть A : X ® Y – ограниченный линейный оператор (X, Y – банаховы пространства). Задача заключается в том, чтобы установить, имеет ли уравнение A x = y решение x Î X для заданного y Î Y. Иначе говоря, нужно описать образ Im A = { y : y = A x, x Î X } оператора A.

Теорема 6.2. Пусть X и Y – банаховы пространства и A : X ® Y – ограниченный линейный оператор, Im A – его образ. Замыкание образа оператора A совпадает с множеством векторов y, удовлетворяющих условию f (y) = 0 для любого функционала f Î Y' такого, что A' f = 0.

Доказательство. Пусть 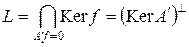– множество векторов, удовлетворяющих условию теоремы. Как пересечение замкнутых линейных подпространств L есть замкнутое подпространство.

Пусть y Î Im A, т. е. y = A x и A' f = 0. Тогда f (y) = f (A x) = A' f (x) = 0, значит, Im A Ì L. Так как L замкнуто, то .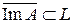

Докажем теперь включение в обратную сторону. Предположим противное, т. е. что существует элемент y ₀ Î L такой, что 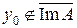. Тогда, согласно следствию 4.3 теоремы Хана – Банаха, существует такой функционал f ₀, что f ₀ (y ₀) ¹ 0 и f ₀ (y) = 0 для всех 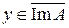. Тогда A' f ₀ (x) = f ₀ (A x) = 0 и условие y ₀ Î L означает, что f ₀ (y ₀) = 0. Полученное противоречие означает, что 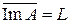. Теорема доказана.

Следствие 6.1. Для того, чтобы уравнение A x = y имело решение, необходимо, а если образ Im A замкнут, то и достаточно, чтобы f (y) = 0 для любого функционала f, удовлетворяющего однородному сопряженному уравнению A' f = 0.

Следствие 6.2. Для того, чтобы уравнение A x = y было разрешимо для любого y Î L, необходимо, чтобы уравнение A' f = 0 имело только нулевое решение.

Доказательство. Если Im A = Y, то, согласно теореме 6.2, для любого y и f Î Ker A' выполнено f (y) = 0, т. е. f = 0. Следствие доказано.

Следствие 6.3. Уравнение A' f = 0 имеет единственное решение тогда и только тогда, когда .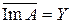

Теорема 6.3. Оператор A : X ® Y имеет ограниченный обратный
A ^{– 1} : Y ® X тогда и только тогда, когда существует постоянная C > 0 такая, что справедливы неравенства

|| x || £ C || Ax ||, x Î X, (2)

|| f || £ C || A' f ||, f Î Y'. (3)

Доказательство. Необходимость. Неравенства ограниченности для операторов A ^{– 1} и (A' ) ^{– 1} совпадают с неравенствами (2) и (3).

Достаточность. Из (3) получаем, что Ker A' = {0}. Тогда по следствию 6.3 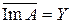. Применяя теперь теорему 2.1 об обратных операторах, получаем существование ограниченного оператора A ^{– 1}. Теорема доказана.

Замечание 6.3. В отличие от конечномерного случая разрешимость уравнения A x = y для любой правой части в бесконечномерном пространстве не связана с единственностью решения этого уравнения. Например, пусть A – оператор одностороннего сдвига влево A : l ₂ ® l ₂, A (x ₁, x ₂, ¼) = (x ₂, x ₃, ¼), Im A = l ₂, Ker A ¹ {0}.