Теорема 4.5 (теорема о дополнениях)

1. Если L – n -мерное подпространство банахова пространства X, то для L существует замкнутое дополнение, которое может быть задано с помощью n линейно независимых функционалов.

2. Если M – замкнутое подпространство в банаховом пространстве X, заданное конечным набором из n линейно независимых функционалов M = { x : f_i (x) = 0, i = 1, 2, ¼, n }, то для M существует дополнение размерности n.

Доказательство. 1. В пространстве L выбираем базис e ₁, e ₂, ¼, e_n. По следствию 4.4 теоремы Хана – Банаха существуют такие линейные ограниченные функционалы f_i, i = 1, 2, ¼, n, что

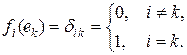
Тогда множество M = { x : f_i (x) = 0, i = 1, 2, ¼, n } является замкнутым дополнением к подпространству L. Действительно, M – замкнутое линейное подпространство и в формуле x = x ₁ + x ₂, где 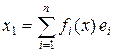, , 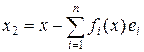имеем x ₁ Î L, x ₂ Î M. Докажем единственность разложения. Если 0 = x ₁ + x ₂, где x ₁ Î L, x ₂ Î M, то 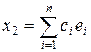. Тогда c_k = f_k (x ₂) = 0, k = 1, ¼, n, т. е. x ₁ = 0, x ₂ = 0. Таким образом, X = L Å M и утверждение 1) доказано.

2. Пусть f ₁,¼, f_n – набор линейно независимых функционалов. Покажем, что отображение F : X ® R ⁿ, определенное формулой

F (x) = ( f ₁(x),¼, f_n (x)),

сюръективно. Если предположим, что Im F ¹ R ⁿ, то существует вектор a = ( a ₁,¼, a _n) Î R ⁿ, a ¹ 0, такой, что 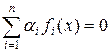для любого x, т. е. функционалы f_i линейно зависимы. Получаем противоречие с условием.

В силу сюръективности F существуют такие e ₁,¼, e_n Î X, что f_i (e_k) = d _{i k}. Тогда, как показано в первой части теоремы, n -мерное подпространство 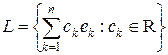является дополнением к M. Теорема доказана.