Линейные ограниченные функционалы в гильбертовом пространстве

Согласно теореме Рисса, любой линейный ограниченный функционал единственным образом представляется в виде f (x)=(x, u), причем || f ||=|| u ||.

5.3. Линейные ограниченные функционалы в пространстве c₀

Пусть e_k =(0,¼,0,1,0,¼), k =1,2,¼ – последовательность элементов из c ₀. Тогда любой элемент x Î c ₀ представляется в виде 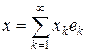, где ряд сходится по норме c ₀. Действительно, 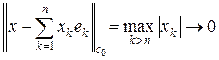при n ®¥. Пусть f – произвольный линейный ограниченный на c ₀ функционал. Тогда

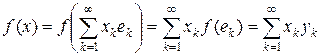Таким образом, функционал f определяется последовательностью чисел y ={ y_k }. Покажем, что y Î l ₁. Положим x ⁽ ⁿ ⁾=(sign y ₁,¼,sign y_n,0,¼)Î c ₀. Тогда 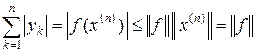. Значит, ряд 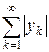сходится и .

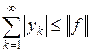Покажем, что для любой последовательности y ={ y_k }Î l ₁ формула 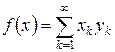определяет линейный ограниченный функционал на c ₀. Действительно, имеем 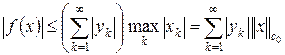. Отсюда следует, что функционал f определен (ряд сходится) и ограничен, причем 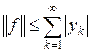. Линейность очевидна. Полученный результат сформулируем в виде теоремы.

Теорема 5.1. Пространство (c ₀) ' линейно изометрично пространству l ₁. Этот изоморфизм задается формулой

l ₁' y ={ y_k }® f Î (c ₀) ', .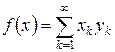

5.4. Линейные ограниченные функционалы в пространстве l₁

Как в случае пространства c ₀, получаем, что любой элемент x Î l ₁ представляется в виде 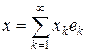(так как 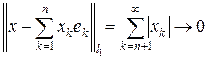при n ®¥), ограниченный линейный функционал f – в виде 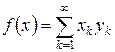, где y_k = f (e_k). Положим x = e_k. Тогда | y_k |=| f (e_k)|£|| f ||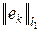=|| f ||, т. е. последовательность y ={ y_k } ограничена числом || f ||. Таким образом, ограниченным линейный функционал f определяется ограниченной числовой последовательностью y ={ y_k }. Покажем, что верно и обратное, т. е. любая ограниченная числовая последовательность { y_k } по формуле 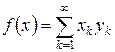определяет ограниченный линейный функционал на пространстве l ₁. Действительно, 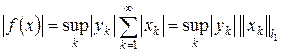, откуда следует, что функционал определен и ограничен, причем 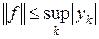. Учитывая неравенство в обратную сторону, имеем 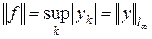. Значит, справедлива

Теорема 5.2. Пространство (l ₁) ' линейно изометрично пространству l _¥. Этот изоморфизм задается формулой

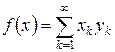5.5. Линейные ограниченные функционалы в пространстве l_p (1<р<+¥)

Теорема 5.3. Пространство (l_p) ' при 1< р <+¥ изометрично пространству l_q, где 1/ p +1/ q = 1. Этот изоморфизм задается формулой

l_q ' y ={ y_k }® f Î (l_p) ', .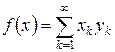

Доказательство. Пусть y ={ y_k }Î l_q. Тогда по неравенству Гёльдера 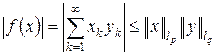, т. е. функционал f ограничен и .

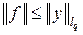Любой элемент x Î l_p представляется в виде 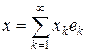(так как 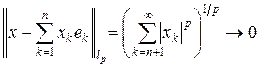при n ®¥). Тогда любой ограниченный функционал f в пространстве l_p представляется в виде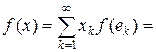
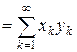. Положим

x ⁽ ⁿ ⁾=(| y ₁| ^q ^–¹sign y ₁,¼,| y_n | ^q ^–¹sign y_n,0,¼)Î l_p.

Тогда

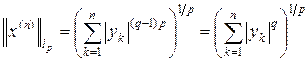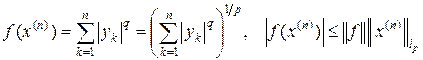Отсюда получаем

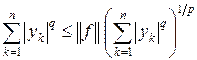или, разделив на 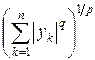, получим 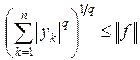. Значит, ряд 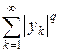сходится и 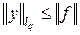. Теорема доказана.

Замечание 5.1. Ограничение р <+¥ в теореме 5.3 существенно, так как пространство (l _¥) ' устроено значительно сложнее и, в частности, не все функционалы на l _¥ представляются в виде .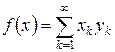

5.6. Линейные ограниченные функционалы в пространстве L_p(T,m) (1<р<+¥)

Теорема 5.4. Пусть T – пространство с полной s -конечной мерой. Пространство (L_p (T, m)) ' при 1< р <+¥ линейно изометрично пространству L_q (T, m), где 1/ p +1/ q = 1. Изоморфизм задается формулой

L_q (T, m)' u ® f Î (L_p (T, m)) ', .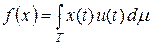

Доказательство. Согласно неравенству Гёльдера, если u Î L_q (T, m) и x Î L_p (T, m), то x u Î L ₁(T, m) и 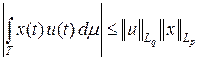. Значит, функционал f задан для любого x Î L_p (T, m), линеен, ограничен и 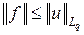. Поэтому для доказательства теоремы достаточно показать, что любой ограниченный линейный функционал f представляется в указанном виде и справедливо неравенство .

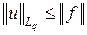Сначала рассмотрим случай m (T)<+¥. Пусть f – ограниченный линейный функционал на L_p (T, m). Пусть A – измеримое множество, его характеристическая функция c_A принадлежит L_p (T, m) и, значит, определено f (c_A). Получаем отображение n : A ® f (c_A). Покажем, что n есть заряд на алгебре измеримых множеств (в смысле определения 3.2), т. е. обладает свойством s -аддитивности. Если 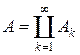, то 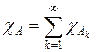, причем ряд сходится в L_p (T, m). В силу линейности и непрерывности f получаем

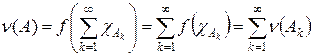Если m (A)=0, то c_A есть нулевой элемент пространства L_p (T, m). Это значит, что заряд n абсолютно непрерывен относительно меры m. По лемме 3.5 существует такая функция u Î L ₁(T, m), что .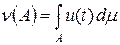

Покажем, что u Î L_q (T, m) и что

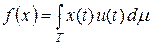. (1)

Представление (1) справедливо для характеристических функций, так как

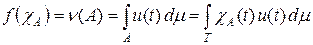В силу линейности представление (1) справедливо для линейных комбинаций характеристических функций, т. е. для простых функций с конечным числом значений. Для ограниченной измеримой функции x построим последовательность x_n простых функций с конечным числом значений, равномерно сходящуюся к x. Переходя к пределу в представлении 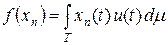, что допустимо в силу теоремы Лебега (теорема 6.3 курса «Функциональный анализ. Часть 1»), получаем представление (1) для ограничейных функций.

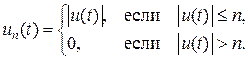
Функция x_n (t)= u_n (t) ^q ^–¹sign u_n (t), ограниченная, измеримая и

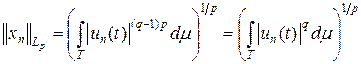В силу представления (1)

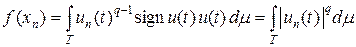Так как 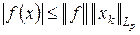, получаем 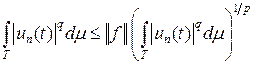. Разделив это неравенство на 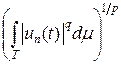, имеем 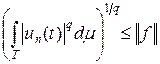. Последовательность | u_n (t)| ^q сходится точечно к | u (t)| ^q и справедлива оценка 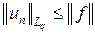. По теореме Фату (теорема курса «Функциональный анализ. Часть 1») получаем, что | u (t)| ^q – интегрируемая функция и

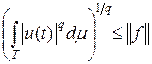т. е. u Î L_q (T, m) и .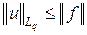

Ограниченный линейный функционал f совпадает с ограниченным линейным функционалом 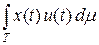на плотном множестве ограниченных функций и, значит, по теореме о продолжении, эти функционалы совпадают на всем L_p (T, m), т. е. справедливо представление (1).

Пусть теперь мера s -конечна, т. е. 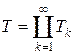, где m (T_k)<+¥. Рассмотрим сужение функционала f на пространство L_p (T_k, m), состоящее из функций, обращающихся в нуль вне множества T_k. По доказанной части теоремы получаем представление 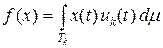, где u_k Î L_q (T_k, m). Аналогично доказательству в разделе 5.5 для пространства (l_p) ' получаем, что ряд 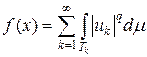сходится, т. е 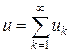Î L_q (T, m). Если 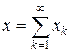, где x_k Î L_p (T_k, m), то

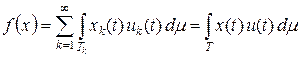Теорема доказана.

5.7. Линейные ограниченные функционалы в пространстве L₁(T,m)

Теорема 5.5. Пространство (L ₁(T, m)) ' при 1< р <+¥ линейно изометрично пространству L _¥(T, m). Этот изоморфизм задается формулой

L _¥(T, m)' u ® f Î (L ₁(T, m)) ', .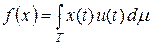

Доказательство этой теоремы в основном аналогично доказательству теоремы 5.4.

5.8. Линейные ограниченные функционалы в пространстве C[0,1]

Рассмотрим подробнее заряды на s -алгебре, порожденной полуинтервалами на отрезке [0,1]. Каждому заряду n (как и мере) на этой s -алгебре поставим в соответствие функцию F (t)= n ([0, t)), F (0)=0. Опишем класс функций на [0,1], которые соответствуют зарядам.

Определение 5.1. Функция g : [ a, b)®R называется функцией ограниченной вариации, если существует число c такое, что для любого разбиения a = t ₀< t ₁<¼< t_n < b справедливо неравенство

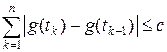. (2)

Наименьшая из постоянных c, при которых справедливо неравенство (2), называется вариацией функции g на полуинтервале [ a, b) и обозначается .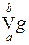

По определению

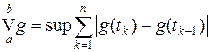где верхняя грань берется по множеству разбиений [ a, b).

Пример 5.1. Монотонная функция g является функцией ограниченной вариации и 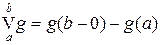. Если функция g непрерывна слева, то .

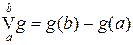Пример 5.2. Если g (t)= g ₁(t)– g ₂(t), где g ₁, g ₂ – монотонно возрастающие функции, то g является функцией ограниченной вариации.

Справедливо и обратное утверждение. Действительно, пусть g (t) – функция ограниченной вариации. Тогда функция 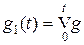монотонно возрастает. Так как 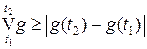, то функция 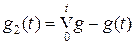тоже возрастает, ибо если t ₁< t ₂, то

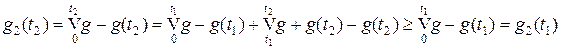Отсюда получаем разложение g (t)= g ₁(t)– g ₂(t). Заметим, что если функция g непрерывна слева, то построенные функции g ₁ и g ₂ непрерывны слева.

Пример 5.3. Функция

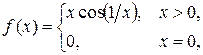
непрерывна на отрезке [0,1]. Если выбрать точки разбиения x_k =1/ kp, то

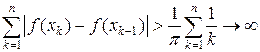
и, значит, f не является функцией ограниченной вариации.

Лемма 5.1. Функция g : [0,1]®R соответствует некоторому заряду n по формуле g (t)= n ([0, t)), тогда и только тогда, когда 1) g – функция ограниченной вариации; 2) g (0)=0; 3) g непрерывна слева.

Доказательство. Пусть функция g построена по некоторому заряду n. Тогда по лемме 3.2 n = m ₁– m ₂, где m ₁, m ₂ – меры. Мерам m ₁ и m ₂ соответствуют функции g ₁ и g ₂ монотонные, непрерывные слева и такие, что g ₁(0)= g ₂(0)=0 (теорема 4.2 курса «Функциональный анализ. Часть 1»). Тогда g (t)= g ₁(t)–
– g ₂(t) удовлетворяет требуемым условиям. Обратно, если g – функция ограниченной вариации, то g (t)= g ₁(t)– g ₂(t), где g ₁ и g ₂ – монотонные непрерывные слева функции. Причем их можно выбрать так, чтобы g ₁(0)= g ₂(0)=0. Поэтому им соответствуют меры m ₁ и m ₂ и, следовательно, функции g соответствует заряд n = m ₁– m ₂. Лемма доказана.

Общий вид линейного ограниченного функционала на пространстве C [0, 1] описывается следующей теоремой.

Теорема 5.6 (Рисс). Для любого ограниченного линейного функционала f на пространстве C [0, 1] существует функция g ограниченной вариации такая, что функционал f представляется с помощью интеграла Римана–Стилтьеса

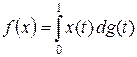, (3)

причем .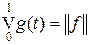

Доказательство. Пусть f – ограниченный линейный функционал на C [0, 1]. Если в интеграле 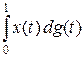подставить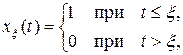

то 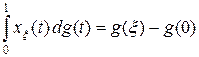, т. е. по значениям интеграла на функциях x_x (t) функция g может быть записана явно. Но функция x_x (t) разрывна и значение функционала f на ней не определено. Поэтому поступаем следующим образом.

Пространство C [0, 1] является подпространством пространства B [0, 1] всех ограниченных функций на [0, 1] с нормой 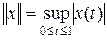. Согласно теореме Хана–Банаха, функционал f может быть продолжен на все пространство с сохранением нормы. Пусть F – такое продолжение. Тогда определено значение F (x_x). Покажем, что функция g (x)= F (x_x) искомая. Возьмем произвольное разбиение отрезка [0, 1], 0= t ₀< t ₁<¼< t_n <1, и составим сумму

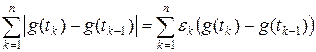где e _k =sign[ g (t_k)– g (t_k _– ₁)]. Тогда

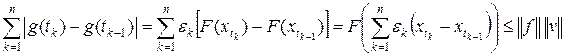где 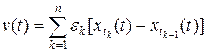. Так как в последней сумме в каждой точке t лишь одно слагаемое может быть отличным от нуля и каждое слагаемое 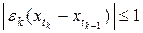, получаем || v ||=1. Значит, функция g имеет ограниченную вариацию и .

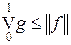Покажем, что справедливо представление (3). Для функций x_x равенство 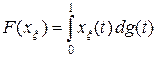справедливо по построению. По линейности равенство распространяется на кусочно-постоянные и непрерывные справа функции – линейные комбинации функций x_x. Если y_n – последовательность кусочно-постоянных непрерывных справа функций, равномерно сходящаяся к непрерывной функции x, то, переходя к пределу в представлении 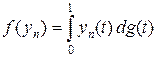, получаем представление (3) для x Î C [0, 1]. Оценим интегральную сумму интеграла Римана–Стилтьеса :

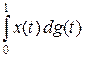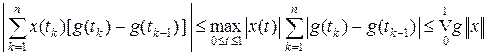Переходя к пределу, получаем 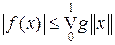, откуда 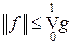. Значит, 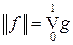. Теорема доказана.

Полученное в теореме 5.6 соответствие не является взаимно однозначным. Так, если g ₁(t)= g (t)+const, то интеграл в (3) не изменится. Не влияет на интеграл для непрерывной функции x также изменение функции g в счетном числе точек. Так как функция ограниченной вариации может иметь не более счетного числа точек разрыва, то, изменив значения функции в этих точках, можно сделать g непрерывной слева. Следующая теорема показывает, что в этом случае соответствие оказывается биективным.

Теорема 5.7. Пространство (C [0, 1]) ' изоморфно пространству V[0,1] функций ограниченной вариации, непрерывных слева и удовлетворяющих условию g (0)=0 с нормой 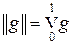. Изоморфизм устанавливается формулой

V[0,1]' g ® f Î (C [0, 1]) ', 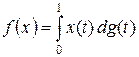. (4)

Доказательство. Пусть g – функция ограниченной вариации. Тогда функционал 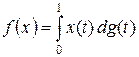на C [0, 1] определен и ограничен, причем 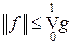. Покажем, что если g непрерывна слева, то 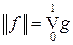. Возьмем e >0 и построим разбиение отрезка [0,1] так, чтобы 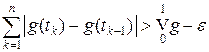. Построим последовательность непрерывных функций x_n таких, что | x_n (t)|£1 и x_n (t)® x ₀(t), где x ₀(t)=sign[ g (t_k)– g (t_k _– ₁)] для t_k _– ₁< t < t_k. В силу леммы 5.1 непрерывной слева функции g (t) соответствует s -аддитивный заряд n на [0,1], поэтому 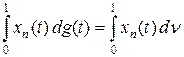. По теореме Лебега (теорема 6.3 курса «Функциональный анализ. Часть 1») возможен предельный переход под знаком интеграла

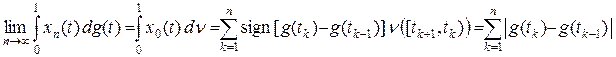Поэтому при достаточно большом n имеем 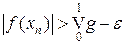и, так как || x_n ||£1, получаем 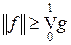. Значит, 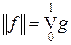и мы показали, что отображение из V[0,1] в (C [0, 1]) ', определенное формулой (4), изометрично и, в частности, инъективно. Сюръективность этого отображения установлена в теореме 5.6. Значит, отображение, определенное формулой (4), является изоморфизмом. Теорема доказана.