Утв.:
Если: 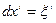 - простейшая дифференциальная форма
- простейшая дифференциальная форма
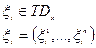
То:
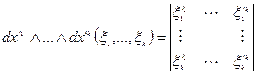
координатная запись простейшей 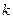 - формы.
- формы.
Координатная запись кососимметрической формы.
Утв.:
Если: 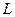 - кососимметрическая форма,
- кососимметрическая форма,
То: 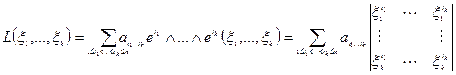
Координатная запись дифференциальной формы.
Утв.:
Если: 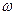 -дифференциальная форма
-дифференциальная форма
То: 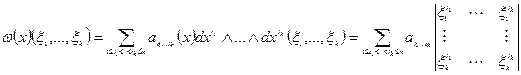
Т.о., произвольная дифференциальная 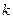 -форма есть линейная комбинация простейших дифференциальных форм.
-форма есть линейная комбинация простейших дифференциальных форм.
Пример:
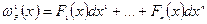
Задача: посчитать значение 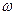 на векторах
на векторах 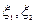 .
.
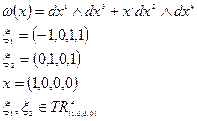
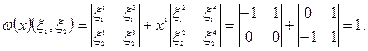
Пример:
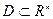
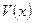 - векторное поле.
- векторное поле.
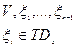
Строим параллелепипед на этих векторах. Ориентированный объём этого параллелепипеда – определитель из координат этих векторов. Разложив его по 1-й строке, получаем:
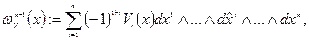
где 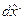 обозначает отсутствие
обозначает отсутствие 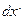 .
.
Форма потока:
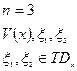
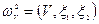 -форма потока.
-форма потока.
Если 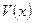 - скорость течения жидкости, протекающей через площадку, натянутую на векторы
- скорость течения жидкости, протекающей через площадку, натянутую на векторы 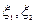 за единицу времени.
за единицу времени.
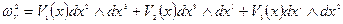
Дифференциал формы.
Опр.:
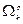 - пространство
- пространство 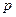 -форм гладкости
-форм гладкости 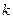
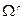 - пространство
- пространство 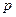 -форм гладкости
-форм гладкости 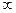 .
.
Опр.:
Внешним дифференциалом называется линейный оператор 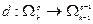 , если:
, если:
1) если 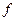 -функция (
-функция (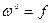 , функция – это 0-форма), то
, функция – это 0-форма), то 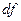 -обычный дифференциал функции.
-обычный дифференциал функции.
2) 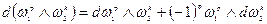
3) 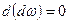
Координатное представление внешнего дифференциала.
Утв.:
Если: 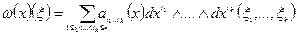
То: 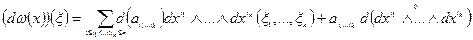
Т.о. при дифференцировании формы нужно продифференцировать её коэффициенты.
Пример 1:
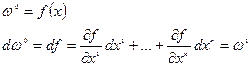
Пример 2:
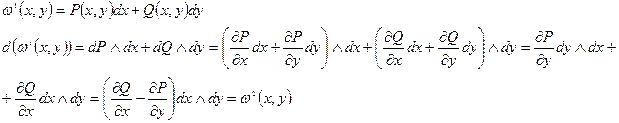
 2014-02-09
2014-02-09 1275
1275
