Алгебра форм

Опр.:

Если: 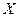- линейное пространство

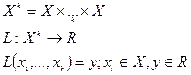
То:

1. 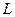называется формой размерности 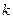(формой, тензором), если она является полилинейной формой, т.е. формой, линейной относительно каждого аргумента:

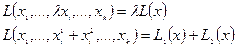
2. при 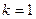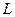называется линейной формой.

при 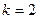- билинейной

Пример:

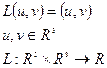
Опр.1:

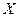- конечномерное

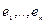- базис в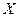

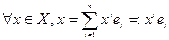
Опр.2:

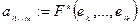
Утв.:

Если: 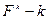-форма

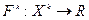
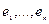- базис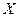

То: 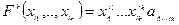(т.е. форма однозначно определяется набором чисел ).

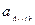Док-во:

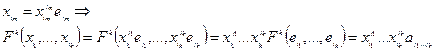
Замечание:

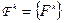- линейное пространство

1)

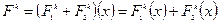
2)

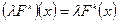
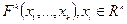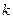- -форма

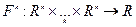
Опр.:

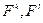- формы

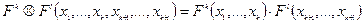
операция 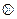называется тензорным произведением.

Свойства:

1.

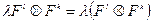
2.

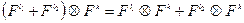
3.

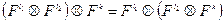
Замечание

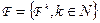
Множество 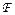всех 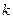-форм на линейном пространстве 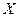является градуированной алгеброй.

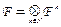
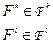
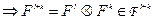
Опр.:

Если: 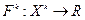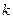-формы

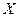- линейное пространство

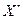- множество линейных функций 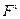, определённых на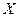

То: 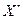называется пространством, сопряжённым пространству .

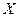Опр.:

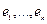- базис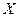

Базис 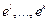пространства 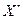называется взаимным (сопряженным) базису 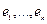, если:

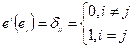
Утв.:

Если: 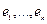- базис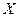

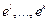- сопряженный ему базис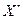

То: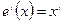

Док-во:

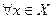
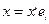
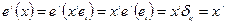
Опр.:

оператор 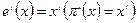называется оператором проектирования