Опр.:
1. Форма 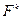 называется кососимметрической, если:
называется кососимметрической, если:
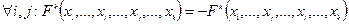
2. 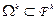 - подпространство кососимметрических форм размерности
- подпространство кососимметрических форм размерности 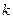
Пример:
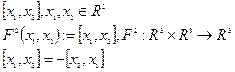
Альтернирование форм
Опр.:
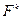 - форма размерности
- форма размерности 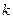
Оператор 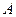 называется оператором альтернирования, если:
называется оператором альтернирования, если:
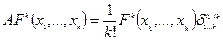
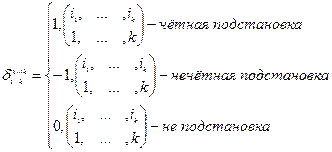
Утв.:
Если: 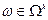
То: 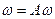 - Операция альтернирования переводит кососимметрическую форму саму в себя.
- Операция альтернирования переводит кососимметрическую форму саму в себя.
Свойства:
1. 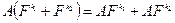
2. 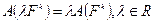
Пример:
1. 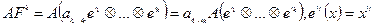
2. а) 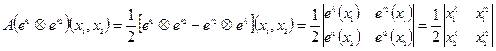
б) 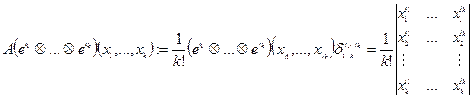
Опр.:
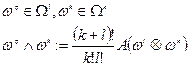
Операция 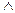 - внешнее произведение.
- внешнее произведение.
Пример:
1. 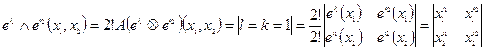
2. 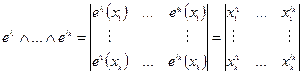
3. 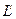 -
- 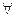 1-форма
1-форма
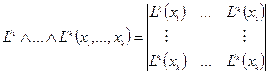
Свойства:
1. 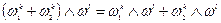
2. 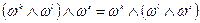
3. 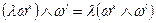
4. 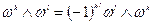
Координатная запись кососимметрической формы.
Утв.:
Если: 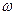 - кососимметрическая форма
- кососимметрическая форма
То: 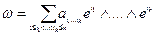
Док-во:
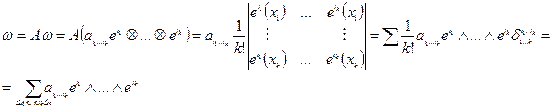
Следствие:
Т.к. 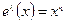 , то
, то 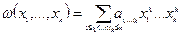
Замечание
Множество кососимметрических форм 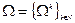 является градуированной алгеброй.
является градуированной алгеброй.
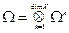
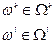
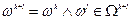
Замечание
1. В силу определения кососимметрической формы, она равна нулю, если в ней есть одинаковые элементы.
2. 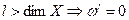
 2014-02-09
2014-02-09 583
583








