Выражение формы объёма в декартовых координатах
Утв.:
Если: 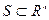 - поверхность размерности
- поверхность размерности 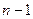 ,
,
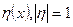 - единичный вектор нормали.
- единичный вектор нормали.
То: 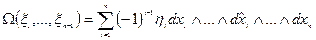
Док-во:
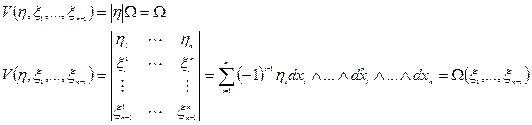
Утв.:
Если: 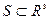 - поверхность размерности 2,
- поверхность размерности 2,
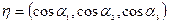 - нормаль
- нормаль
То: 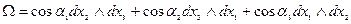
Док-во:
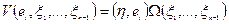
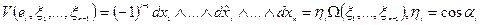
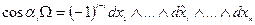
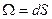
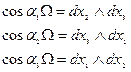
Опр.:
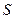 - ориентированная поверхность
- ориентированная поверхность
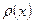 - функция
- функция
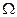 - форма объёма
- форма объёма
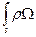 - интеграл I рода по ориентированной поверхности
- интеграл I рода по ориентированной поверхности 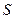
Пример:
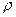 - плотность
- плотность
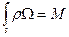 - масса
- масса
Замечание:
Изменение ориентации не меняет интеграл I рода, т.к. при изменении ориентации поверхности изменяется и форма объёма.
Замечание:
Т.к. 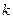 -мерные кососимметрические формы размерности
-мерные кососимметрические формы размерности 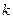 пропорциональны между собой, то любой интеграл II рода может быть представлен через интеграл I рода.
пропорциональны между собой, то любой интеграл II рода может быть представлен через интеграл I рода.
Примеры:
1. 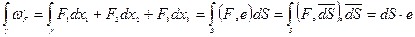
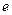 - касательный вектор к кривой
- касательный вектор к кривой 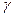
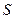 - натуральный параметр
- натуральный параметр
2. 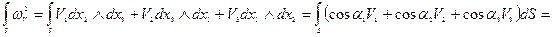
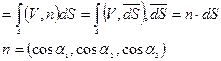
 2014-02-09
2014-02-09 388
388








