Интеграл от формы потока
Интеграл от формы работы.
Интегралы от формы работы, потока. Форма объёма.
Если: 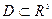
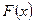 -поле (силовое)
-поле (силовое)
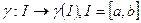
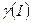 - параметризованная кривая
- параметризованная кривая
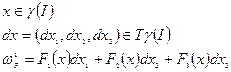
То: 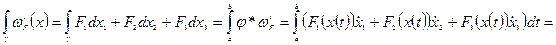
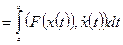
Если: 
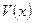 - поле скоростей
- поле скоростей
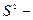 ориентированная поверхность
ориентированная поверхность
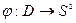 - её карта
- её карта
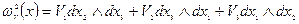
То:
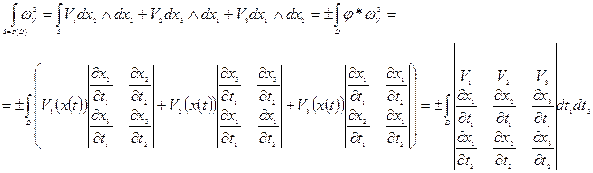
Опр.:
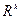 - ориентированное евклидово пространство со скалярным произведением.
- ориентированное евклидово пространство со скалярным произведением.
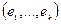 -репер
-репер
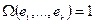
Формой объёма на 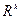 называется кососимметрическая
называется кососимметрическая 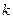 -форма, которая на ортонормированном репере данного класса ориентации принимает значение единица.
-форма, которая на ортонормированном репере данного класса ориентации принимает значение единица.
Утв.:
Определение корректно J
Док-во:
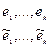
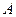 -матрица перехода,
-матрица перехода, 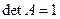
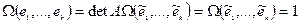
Утв.:
Значение формы объёма на наборе векторов 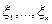 - ориентированный объём параллелепипеда, натянутого на эти вектора.
- ориентированный объём параллелепипеда, натянутого на эти вектора.
Док-во:
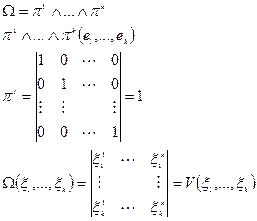
Опр.:
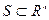
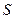 -гладкая поверхность размерности
-гладкая поверхность размерности 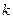
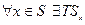
Пусть в касательном пространстве ориентация согласована с исходной ориентацией пространства 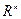 , тогда форма объёма в
, тогда форма объёма в 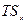 называется формой объёма на поверхности
называется формой объёма на поверхности 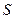 .
.
Опр. 1:
Площадью поверхности 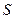 называется
называется 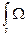
Замечание:
Площадь поверхности не зависит от ориентации, т.к. при изменении ориентации меняется и форма объёма.
Опр. 2:
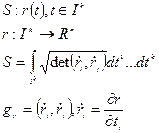
Утв.: опр.1 эквивалентно опр.2.
Док-во:
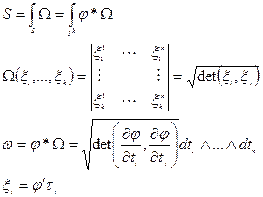
Опр.:
Если 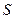 -кусочно-гладкая поверхность, состоящая из гладких частей
-кусочно-гладкая поверхность, состоящая из гладких частей 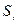 , пересекающихся по поверхностям размерности не выше, чем
, пересекающихся по поверхностям размерности не выше, чем 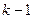 , то площадь
, то площадь 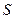 = сумме площадей
= сумме площадей 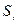 .
.
 2014-02-09
2014-02-09 1231
1231








