Элементы векторного анализа
1. Скалярные и векторные поля.
Опр.:
1) 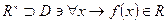 - скалярное поле
- скалярное поле
2)  - векторное поле
- векторное поле
3) 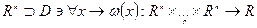 - поле форм
- поле форм
2. Связь между векторными полями и формами в 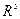
Утв.:
Если: 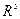 - ориентированное евклидово пространство,
- ориентированное евклидово пространство,  - векторные поля,
- векторные поля,
То: полю  соответствует линейная (билинейная) форма.
соответствует линейная (билинейная) форма.
Док-во:
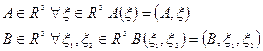
Утв.:
Задание в области 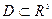 ориентированного евклидова пространства
ориентированного евклидова пространства 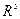 дифференциальной формы эквивалентно заданию в этой области векторных полей
дифференциальной формы эквивалентно заданию в этой области векторных полей 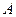 и
и 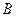 .
.
Док-во:
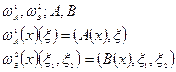
Замечание: в случае скалярного поля:
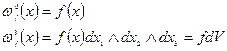
3. Дифференциальные операторы градиент, ротор и дифергенция.
Опр.:
Внешнему дифференцированию 0,1,2 – форм в ориентированном евклидовом пространстве 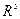 отвечают операции нахождения градиента скалярного поля и нахождения ротора и дивергенции векторных полей, определённых соотношениями:
отвечают операции нахождения градиента скалярного поля и нахождения ротора и дивергенции векторных полей, определённых соотношениями:
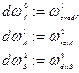
Запись в декартовых координатах
1. 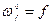
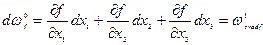
2. 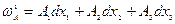
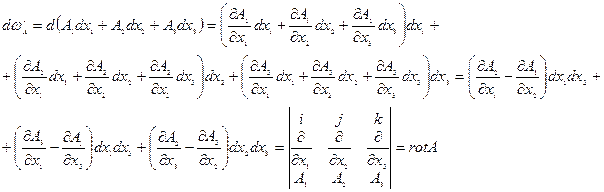
3. 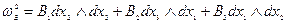
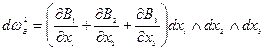
 2014-02-09
2014-02-09 710
710







