Приоритет - предпочтение в обслуживании.
Заявки 1-го типа имеют приоритет (абсолютный) над заявками 2-го типа.
Абсолютный приоритет предполагает, что заявка вытесняет с обслуживания заявку, имеющую более низкий приоритет.
1. Введём множество состояний:
S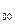 - система пуста.
- система пуста.
S - 1 заявка 1го типа и 0 заявок 2го типа.
- 1 заявка 1го типа и 0 заявок 2го типа.
S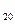 - 2 заявки 1го типа и 0 заявок 2го типа.
- 2 заявки 1го типа и 0 заявок 2го типа.
S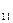 - 1 заявка 1го типа и 1 заявка 2го типа.
- 1 заявка 1го типа и 1 заявка 2го типа.
S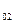 - 0 заявок 1го типа и 2 заявки 2го типа.
- 0 заявок 1го типа и 2 заявки 2го типа.
S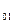 - 0 заявок 2го типа и 2 заявки 2го типа.
- 0 заявок 2го типа и 2 заявки 2го типа.
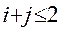
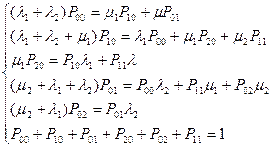
Вероятность отказа заявки 1го и 2го типов:
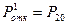
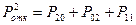
Абсолютная пропускная способность: 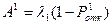
Заявки 2го приоритета вытесняются:
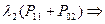

Среднее число каналов занятых обслуживанием:
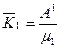
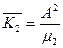
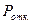 - произвольно взятая заявка получит отказ.
- произвольно взятая заявка получит отказ.
Гипотезы:
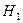 - поступила заявка 1го типа.
- поступила заявка 1го типа.
 - поступила заявка 2го типа.
- поступила заявка 2го типа.
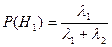
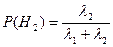
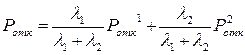 .
.
Все характеристики для заявок 1го типа могут быть получены, игнорируя заявки 2го типа и, рассматривая задачу так, как будто на 2х канальную СМО с отказами поступают заявки только 1го типа.
Отказы технических устройств
Будем считать, что устройства дублированы.
Отказавшее устройство восстанавливается.
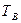 - среднее время восстановления.
- среднее время восстановления.
Найти долю времени, когда устройство работает.
1. Введем множество состояний:
S0- оба устройства исправны.
S1- одно устройство ремонтируется, другое исправно.
S2- оба устройства ремонтируются.
2. Построим граф состояний:
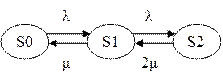
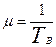
По формулам Эрланга:
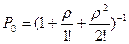
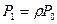
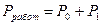
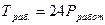 (в часах).
(в часах).
Системы типа M/D/1; M/Er/1; M/G/1
Это более сложные модели массового обслуживания, которые предполагают, что закон обслуживания не является экспоненциальным. В этом случае уже не удается свести их к схеме гибели и размножения. Для решения используется более сложный математический аппарат вложенных цепей Маркова. В результате использования этого аппарата получена формула Поллачека-Хинчина:
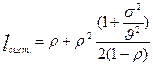
 - число заявок в СМО.
- число заявок в СМО.
Коэффициент вариации времени обслуживания: 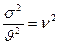
1.) Система типа M/D/1 с постоянным обслуживанием.
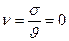

2.) Система типа M/M/1 с экспоненциальным обслуживанием.
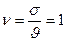
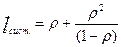
3.) Система типа M/Er/1 с «эрланговским» обслуживанием.
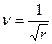 где r- показатель закона Эрланга.
где r- показатель закона Эрланга.
 2014-02-09
2014-02-09 934
934

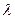 -
- 






