Нахождение локальных экстремумов функций

Примеры использования основных возможностей MathCAD для решения некоторых математических задач

В данном разделе приведены примеры решения задач, для решения которых необходимо решить уравнение или систему уравнений.

Необходимое условие экстремума (максимума и/или минимума) непрерывной функции формулируется так: экстремумы могут иметь место только в тех точках, где производная или равна нулю, или не существует (в частности, обращается в бесконечность). Для нахождения экстремумов непрерывной функции сначала находят точки, удовлетворяющие необходимому условию, то есть находят все действительные корни уравнения .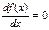

Если построен график функции, то можно сразу увидеть — максимум или минимум достигается в данной точке х. Если графика нет, то каждый из найденных корней исследуют одним из способов.

1-й способ. Сравнение знаков производной. Определяют знак производной 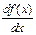вокрестности точки (в точках, отстоящих от экстремума функции по разные стороны на небольших расстояниях). Если знак производной при этом меняется от «+» к «–», то в данной точке функция имеет максимум. Если знак меняется от «–» к «+», то в данной точке функция имеет минимум. Если знак производной не меняется, то экстремумов не существует.

2-й способ. Вычисление второй производной. В этом случае вычисляется вторая производная 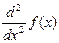в точке экстремума. Если она меньше нуля, то в данной точке функция имеет максимум, если она больше нуля, то минимум.

Пример. Нахождение экстремумов (минимумов/максимумов) функции .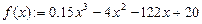

Сначала построим график функции (рис. 6.1).

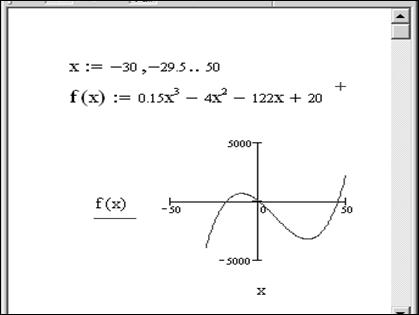
Рис. 6.1. Построение графика функции

Определим по графику начальные приближения значений х, соответствующих локальным экстремумам функции f (x). Найдем эти экстремумы, решив уравнение 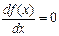. Для решения используем блок Given – Find (рис. 6.2.).

Рис. 6.2. Нахождение локальных экстремумов

Определим вид экстремумов первым способом, исследуя изменение знака производной в окрестности найденных значений (рис. 6.3).

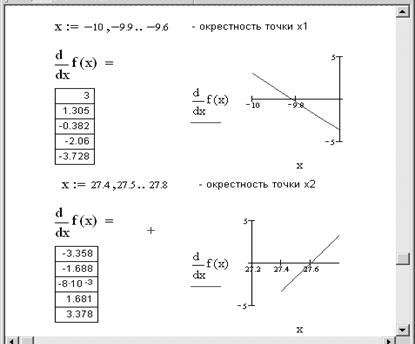
Рис. 6.3. Определение вида экстремума

Из таблицы значений производной и из графика видно, что знак производной в окрестности точки x 1 меняется с плюса на минус, поэтому в этой точке функция достигает максимума. А в окрестности точки x 2 знак производной поменялся с минуса на плюс, поэтому в этой точке функция достигает минимума.

Определим вид экстремумов вторым способом, вычисляя знак второй производной (рис. 6.4).

Рис. 6.4. Определение вида экстремума с помощью второй производной

Видно, что в точке x 1 вторая производная меньше нуля, значит, точка х 1 соответствует максимуму функции. А в точке x 2 вторая производная больше нуля, значит, точка х 2 соответствует минимуму функции.