2015-04-01
1697
Цель: формирование умения находить промежутки возрастания и убывания функции, исследовать функцию на экстремум с помощью производной.
Задание для самостоятельной внеаудиторной работы:
& 18.1. Вспомните определения точки экстремума и экстремума функции. Проанализируйте, в чем заключается их кардинальное отличие. Изучите достаточное условие существования экстремума (критерий нахождения точек экстремума) функции.
& 18.2. Постарайтесь освоить алгоритм, позволяющий находить экстремумы функции.
?18.3. Найдите промежутки возрастания, убывания и экстремумы функции:
а)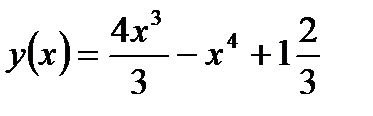 
; б)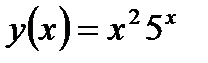 
.
¶ 18.4. Определите, при каком значении a функция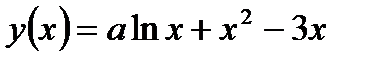 
имеет экстремум в точке 
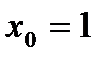. Выясните, будет ли в этом случае данная точка являться точкой максимума или точкой минимума функции.
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
По теореме Ферма (необходимое условие существования экстремума функции), точки экстремума нужно искать среди критических точек. Но не любая критическая точка является точкой экстремума функции. Чтобы выяснить, в каких критических точках функция имеет экстремум, рассмотрим достаточные условия существования экстремума.
Достаточные условия существования экстремума (критерий нахождения точек экстремума): пусть функция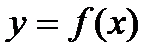 
непрерывна и дифференцируема в некоторой окрестности точки хо. Тогда:
1. если производная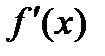 
при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума;
2. если производная 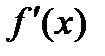при переходе через точку хо меняет знак с минуса на плюс, то точка хо является точкой минимума.
Критерий нахождения точек экстремума функции удобно представляется в виде схемы:
| хо – критическая точка: f`(xо) =0 или f`(xо) не существует | |||
| хо – точка минимума | хо |
| |
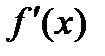| хо – точка максимума | хо |
|
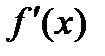Для нахождения экстремумов функции используется следующий алгоритм:
1. Найдите область определения функции.
2. Найдите первую производную функции.
3. Определите критические точки первого рода (f'(xo) =0 или f'(xo) не существует).
4. На числовой оси отметьте критические точки и определите знаки производной на каждом из получившихся интервалов.
5. Выпишите точки экстремума функции (если они есть), используя соответствующие критерии, вычислите значения функции в точках экстремума.
Пример 1. Найдите экстремумы функции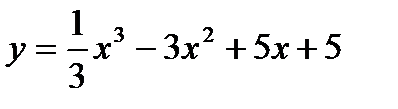 
.
Решение. Воспользуемся решением примера 1 из задания 17. На 4-м шаге мы получили:
| т.min |
| т.max |
| х |
| + |
| + |
|
|
|
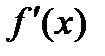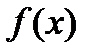5. Согласно критерию нахождения точек экстремума х =1 – точка максимума, х =5 – точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках:
= 
= 
= 
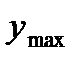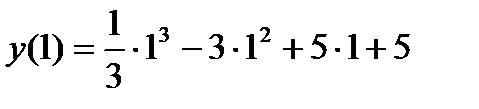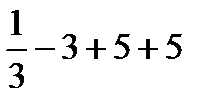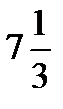- максимум функции;
= 
= 
= 
= 
= 
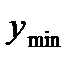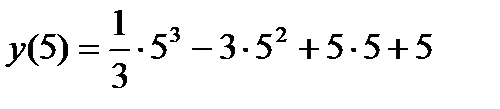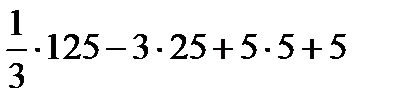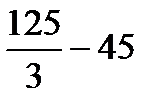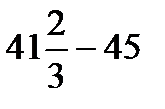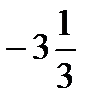- минимум функции.
Ответ: х =1 – точка максимума; =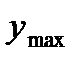 
= ;
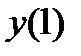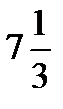х =5 – точка минимума; =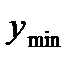 
= .
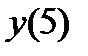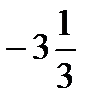Пример 2. Найдите экстремумы функции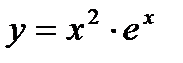 
.
Решение. Воспользуемся решением примера 2 из задания 17. На 4-м шаге мы получили:
| т.min |
| т.max |
| -2 |
| х |
| + |
| + |
|
|
|
|
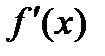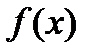5. Согласно критерию нахождения точек экстремума х =-2 – точка максимума, х =0 – точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках:
= 
= 
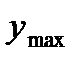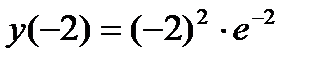
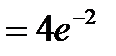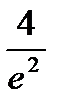- максимум функции;
= 
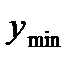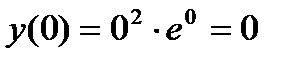- минимум функции.
Ответ: х =-2 – точка максимума; =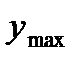 
= ;
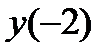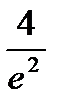х =5 – точка минимума; =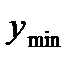 
.
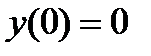Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 6, §6.7, стр. 138 – 141.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 38-39, стр. 220-226.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §7, стр. 255– 265.
