2015-03-07
2609
Многие задачи – как из области математики, так и из других областей науки и техники – приводят к вопросу о нахождении максимального или минимального, наибольшего или наименьшего значений некоторых функций, зависящих от одного и более переменных. Примерами служат задачи вида:
Ø При переноске труб по двум коридорам, пересекающимся под прямым углом, найти наибольший размер трубы, которую можно пронести по коридорам. Ширина обоих коридоров известна.
Ø Определить размеры прямоугольного бассейна данного объема V так, чтобы на облицовку его поверхности потребовалось наименьшее количество материала.
Ø Производственная функция (в денежном выражении) имеет вид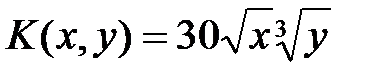 
, где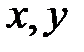 
- количество единиц соответственно первого и второго ресурса. Известна стоимость единицы первого и второго ресурсов. Найти максимальную прибыль при использовании этих ресурсов.
Во многих задачах требуется исследовать функцию на экстремум в случае, когда переменные функции не являются независимыми, а связаны друг с другом некоторыми добавочными условиями, которые служат ограничениями на их использование. В этом случае возникает специфическая задача для функций нескольких переменных на условный экстремум. Например,
Ø Из данного куска жести заданной площади надо сделать гараж в форме параллелепипеда, имеющую наибольшую вместимость.
Ø Производственная функция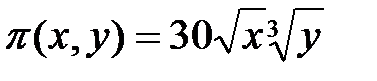 
, стоимость единицы первого ресурса равна 5, второго – 10 ден. ед. В силу бюджетных ограничений на ресурсы может быть потрачено не более 600 ден. ед. В этих условиях найти оптимальное для производителя значение (
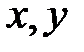) количества используемых ресурсов.
Необходимость решения подобного рода задач требует введения понятий локальных экстремумов, условных экстремумов, глобальных экстремумов и методов их нахождения.
