Собственные значения обратной матрицы.
Пусть
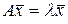 ,
,
т.е. 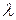 и
и 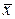 – собственное значение и собственный вектор матрицы
– собственное значение и собственный вектор матрицы 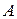 .
.
Умножая обе части данного равенства на 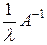 , получим
, получим
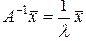 .
.
Следовательно, 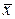 – собственный вектор матрицы
– собственный вектор матрицы 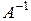 , а
, а 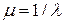 – собственное значение матрицы
– собственное значение матрицы 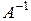 .
.
Пусть даны матрицы 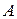 и
и 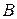 , при этом
, при этом 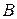 – невырожденная. Требуется найти ненулевой вектор
– невырожденная. Требуется найти ненулевой вектор 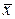 и число
и число 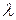 , удовлетворяющие равенству
, удовлетворяющие равенству
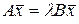 . (2.4.16)
. (2.4.16)
В этом случае 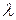 и
и 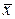 , соответственно, называются обобщенными собственным числом и собственным вектором.
, соответственно, называются обобщенными собственным числом и собственным вектором.
Умножая на 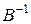 обе части (2.4.16), получим
обе части (2.4.16), получим
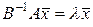 . (2.4.17)
. (2.4.17)
Таким образом, задачу можно свести к определению собственных чисел и векторов матрицы 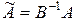 .
.
 2014-02-09
2014-02-09 2117
2117
