Решая систему двух уравнений, найдем

а_В=12p² м/с²: а_ВА^τ= 56 p² м/с²

Угловое ускорение ε _ВА=а_ВА^τ/АВ

ε _ВА=53,9 с^-2

Последовательность графического решения показана на рисунке.

Пример. Колесо радиуса R катится без скольжения по рельсу. Скорость центра в данный момент времени v₀. Определить скорости точек A, B, C, D, P на наружной поверхности колеса.

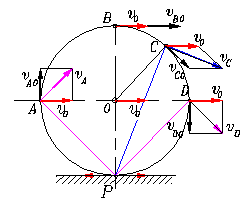Решение. Так как колесо катится без скольжения, скорость в точке касания Р − v_Р= 0. Точка Р является мгновенным центром скоростей. Скорости точек равны произведению угловой скорости на расстояние от точки до полюса и направлены перпендикулярно к линиям, которые соединяют эти точки с полюсом.

v_о= ω РО; v_А= ω РА; v_В= ω РВ; …

Тогда ω= v_о / R

Скорости можно определить, если принять центр колеса т. О за полюс. Скорости остальных точек будут равны геометрической сумме скоростей полюса v_о и скорости вращения этой точки вокруг полюса. Эти скорости направлены перпендикулярно к радиусам и равны ωR.

Решение показано на рис.

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

Относительное, переносное и

абсолютное движения

В ряде случаев целесообразно рассматривать движение точки или тела по отношению к двум системам отсчета, из которых одна считается условно неподвижной, а другая движется по отношению к первой. Сложное движение разлагается на два более простых и более легко исследуемых.

Рассмотрим сложное движение точки М, перемещающейся по отношению к подвижной системе отсчета Oxyz, которая в свою очередь движется относительно другой системы отсчета О₁x₁у₁z₁, которая считается неподвижной. Каждая из этих систем отсчета связана с определенным телом.

Введем следующие определения:

1. Движение, совершаемое точкой М по отношению к подвижным осям координат называется относительным движением. Траектория А В, точки в относительном движении, называется относительной траекторией. Скорость движения точки вдоль этой кривой АВ называется относительной скоростью v_ОТ

Величина, характеризующая изменение относительной скорости v_ОТ точки при ее относительном движении, называется относительным ускорением а_ОТ.

2. Движение, совершаемое подвижной системой отсчета Oxyz и всеми, неизменно связанными с ней, точками пространства по отношению к неподвижной системе Ох₁у₁z₁ является для точки М перенос ным движением.

Скорость точки, связанной с подвижными осями Oxyz, с которой в данный момент совпадает точка М, называется переносной скоростью точки М в этот момент v_ПЕР, а ускорение этой точки — переносным ускорением точки а_ПЕР.

Если представить себе, что относительное движение точки М происходит по поверхности (или внутри) твердого тела, с которым жестко связаны подвижные оси Oxyz, то переносной скоростью (или ускорением) точки М в данный момент будет скорость (или ускорение) той точки тела, с которой в этот момент совпадает точка М.

Переносное ускорение характеризует то изменение переносной скорости v_ПЕР, которое происходит только при переносном движении подвижной системы отсчета.

3. Движение, совершаемое точкой по отношению к неподвижной системе отсчета O\Xyz, называется абсолютным. Траектория CD этого движения называется абсолютной траекторией, скорость — абсолютной скоростью v_а, а ускорение — абсолютным ускорением а_а.

Сложение скоростей.

Рассмотрим точку М, совершающую сложное движение. Пусть эта точка, двигаясь вдоль своей относительной траектории АВ, совершает за промежуток времени ∆t относительное перемещение, определяемое вектором ММ_ОТ

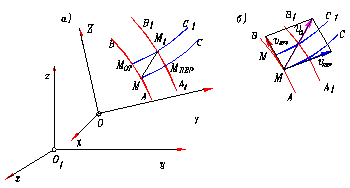
Кривая АВ, двигаясь вместе с подвижными осями OXYZ, перейдет за тот же промежуток времени в какое-то новое положение A₁B₁. Одновременно та точка кривой AВ, с которой в момент ∆ t совпадает точка М, совершит переносное перемещение ММ_ПЕР. В результате этих движений точка М придет в положение М₁.

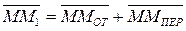
Разделим обе части равенства на ∆ t и перейдя к пределу получим:

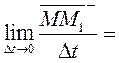
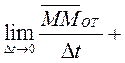
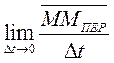
Тогда по определению:

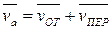
Векторы скоростей направлены по касательным к соответствующим траекториям.

Теорема о сложении скоростей: при сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.

На рис. показан параллелограмм скоростей.

Абсолютная скорость v_а по модулю:

v_а²=v_ОТ²+v_ПЕР²+2 v_ОТv_ПЕРcosα

здесь α − угол между направлениями векторов v_ОТ и v_ПЕР

С помощью параллелограмма скоростей решается ряд задач кинематики точки, а именно:

а) зная скорости v_ОТ и v_ПЕР можно найти абсолютную скорость точки v_а

б) зная v_а и направления скоростей v_ОТ и v_ПЕР можно найти модули этих скоростей;

в) зная скорости v_а и v_ПЕР можно найти относительную скорость точки v_ОТ.

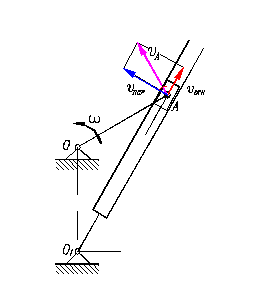
На рис. показан кривошипно-кулисный механизм.

Кривошип ОА вращается вокруг т. О. Абсолютная скорость т. А направлена перпендикулярно к радиусу ОА. По направляющим кулисы перемещается ползун А. Кулиса вращается вокруг т. О₁.

В качестве переносного движения относительно неподвижной системы координат примем вращательное движение кулисы.

Переносной скоростью т. А является скорость точки кулисы, которая в данный момент совпадает с т. А. Эта скорость направлена перпендикулярно к радиусу О₁А.

Относительной скоростью будет скорость скольжения ползуна вдоль кулисы.

Пример. Кривошип ОА вращается вокруг т. О с угловой скоростью ω= 10 с⁻¹;ОА=ОО₁= 0,2 м.

При заданном положении механизма определить угловую скорость кулисы ω_К

Решение. Абсолютная скорость т. А направлена перпендикулярно к радиусу ОА и равна:

v_а= ω ОА= 2 м/с

Переносная скорость т. А v_ПЕР является составляющей абсолютной скорости v_а из параллелограмма скоростей: v_ПЕР=v_аcos 30°=1,73 м/с

Угловая скорость кулисы ω_К:= v_ПЕР / О₁А

В равнобедренном треугольнике О₁ОА О₁А=0,346 м.

Тогда ω_К:=5 с⁻¹.