Рисунок 3.5
Рисунок 3.4
Рисунок 3.3
Найдем ток в первой схеме. Согласно второму законом Кирхгофа имеем одно уравнение: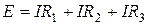 , откуда
, откуда 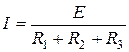 .
.
Но для данной схемы ток можно найти иначе. Обозначим напряжение между точками a и b: 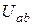 . Тогда для двух условных контуров будем иметь два уравнения:
. Тогда для двух условных контуров будем иметь два уравнения:
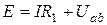 ;
; 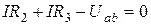 .
.
Из первого получаем закон Ома для участка цепи с источником напряжения:
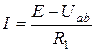 .
.
2. Реальные источники электрической энергии и их эквивалентные схемы.
Выше (лекция 1) был определен идеальный источник напряжения, напряжение на зажимах которого не зависит от тока, который в нем проходит и равняется E.
Реальный источник напряжения - активный элемент, который можно подать в виде идеального источника напряжения и последовательно соединенного с ним пассивного элемента 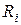 , который учитывает потери энергии в источнике (рис. 3.4а).
, который учитывает потери энергии в источнике (рис. 3.4а).
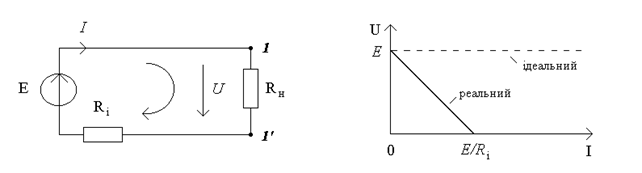
а) б)
По закону Киpхгофа можно записать 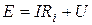 , откуда получаем выражение для вольт-амперной харaктeристики реального источника напряжения:
, откуда получаем выражение для вольт-амперной харaктeристики реального источника напряжения: 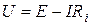 (pис.3.4б). Харaктерные точки ВАХ:
(pис.3.4б). Харaктерные точки ВАХ:  ,
, 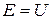 ;
; 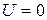 ,
, 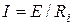 . Штриховой линией изображена ВАХ идеального источника напряжения: Е = const.
. Штриховой линией изображена ВАХ идеального источника напряжения: Е = const.
Выясним, при каких условиях реальный источник приближается к идеальному. Найдем напряжение на зажимах реального источника, к которому подключается сопротивление нагрузки (pис.3.4а):
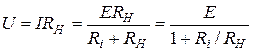 . (3.5)
. (3.5)
Из (3.5) видно, что 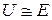 , если отношение
, если отношение 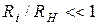 . Итак, чтобы источник напряжения можно было рассматривать как идеальный, необходимо чтобы
. Итак, чтобы источник напряжения можно было рассматривать как идеальный, необходимо чтобы 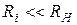 .
.
Реальный источник тока - активный двухполюсник, который состоит из идеального источника тока и параллельно соединенного с ним пассивного элемента 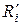 , который учитывает потери (рис. 3.5а).
, который учитывает потери (рис. 3.5а).
Согласно первому закону Кирхгофа можно записать: 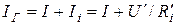 . Это выражение описывает ВАХ реального источника тока (pис.3.5б). Характерные точки ВАХ такие:
. Это выражение описывает ВАХ реального источника тока (pис.3.5б). Характерные точки ВАХ такие: 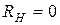 ,
, 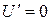 ,
, 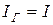 ;
; 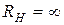 ,
, 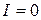 ,
, 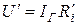 . На том же рисунке штриховой линией показано ВАХ идеального источника тока:
. На том же рисунке штриховой линией показано ВАХ идеального источника тока: 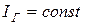 .
.
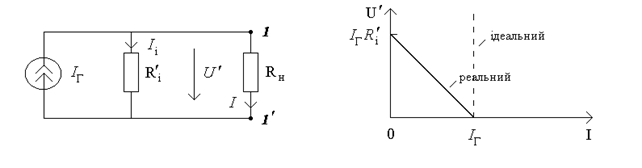
а) б)
Найдем ток в ребре нагрузки, который подключен к реальному источнику тока (рис.3.5а). По формуле разброса токов
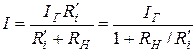 . (3.6)
. (3.6)
По некоторым соотношениям схемы реальных источников напряжения (рис.3.4а) и тока (рис.3.5а) эквивалентны. Выясним, по каким именно? Соответственно к пpинципу эквивалентних преобразований, напряжение во внешней цепи (т.е., на ребре нагрузка) не может изменяться при переходе от схемы (рис.3.4а) к схеме (рис.3.5a): 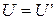 . Для первой схемы:
. Для первой схемы: 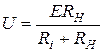 , для второй:
, для второй: 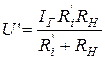 .
.
Если 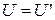 , то
, то 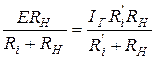 , откуда
, откуда
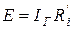 ;
; 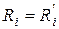 . (3.7)
. (3.7)
Итак, схемы источников тока и напряжения эквивалентны, если выполняются условия (3.7). Такой же вывод можно получить иначе: схемы источников есть эквивалентними, если их ВАХ совпадают.
Сравнивая ВАХ источника напряжения 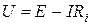 и ВАХ источника тока
и ВАХ источника тока 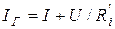 (или
(или 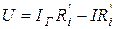
 ), имеем:
), имеем: 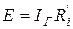 ,
, 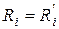 . Анализируя (3.7), делаем вывод: внутренние сопротивления источников напряжения и тока при эквивалентном изменении должны равняться друг другу, ток источника при замене схемы (рис. 3.4а) схемой (рис. 3.5а) будет представлять
. Анализируя (3.7), делаем вывод: внутренние сопротивления источников напряжения и тока при эквивалентном изменении должны равняться друг другу, ток источника при замене схемы (рис. 3.4а) схемой (рис. 3.5а) будет представлять 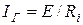 , при обратной замене ЭДС источника напряжения будет равняться
, при обратной замене ЭДС источника напряжения будет равняться 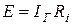 .
.
3. Последовательное соединение n реальных источников (рис.3.6). На основе второго закона Кирхгофа и эквивалентного преобразования последовательно соединенных резисторов будем иметь: 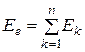 ;
; 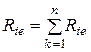 .
.

 2014-02-09
2014-02-09 1886
1886








