Рисунок 4.4
Рисунок 4.3
Рисунок 4.2
Рисунок 4.1
По второму закону Кирхгофа составим уравнения для первого контура
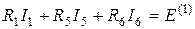 .
.
Выразим токи "внутренних" веток  ,
,  через токи "внешних" веток
через токи "внешних" веток  ,
, 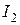 ,
, 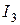 . По первому закону Кирхгофа для узлов 1 и 4 запишем:
. По первому закону Кирхгофа для узлов 1 и 4 запишем:
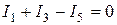 ;
; 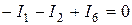 , откуда
, откуда 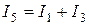 ;
; 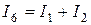 .
.
Тогда уравнения для первого контура примет вид
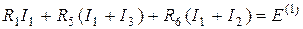 .
.
Сгруппировав слагаемые, будем иметь
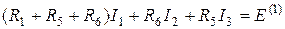 . (4.1)
. (4.1)
Введем понятие контурных токов, контурных ЭДС и ребер. Контурный ток 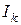 - ток в главной ветке, номер которой совпадает с номером контура и которая есть внешней (
- ток в главной ветке, номер которой совпадает с номером контура и которая есть внешней (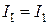 ,
, 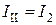 ,
, 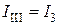 ).
).
Другими словами, это токи внешних веток, которые условно замыкаются в соответствующих контурах. Для удобства будем считать, что направление контурного тока совпадает с направлением обхода соответственного контура. В общем контурные токи - это условные величины, но в отдельных случаях они могут совпадать с токами веток схемы.
Контурная ЭДС k -го контура 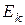 - равняется алгебраической сумме всех ЭДС, которые входят в этот контур. Для рассматриваемого примера
- равняется алгебраической сумме всех ЭДС, которые входят в этот контур. Для рассматриваемого примера
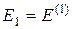 ;
; 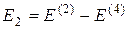 ;
; 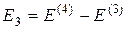 .
.
Собственное сопротивление k -го контура 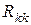 - равняется сумме всех ребер, которые составляют этот контур:
- равняется сумме всех ребер, которые составляют этот контур: 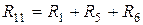 ;
; 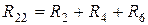 ;
; 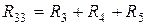 .
.
Взаимное сопротивление k -го и s -го контуров 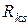 - равняется сопротивлению ветки, которая входит в эти контуры, со знаком "плюс", если направления контурных токов в ней совпадают, и со знаком "минус", если они противоположны. Для схемы (рис.4.1) имеем
- равняется сопротивлению ветки, которая входит в эти контуры, со знаком "плюс", если направления контурных токов в ней совпадают, и со знаком "минус", если они противоположны. Для схемы (рис.4.1) имеем 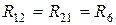 ;
; 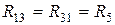 ;
; 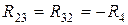 .
.
С учетом введенных обозначений уравнения (4.1) будет таким:
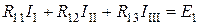 .
.
Записав аналогично уравнения для второго и третьего контуров, получаем систему уравнений, из которой можно определить любой контурный ток
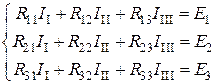 , (4.2)
, (4.2)
или в матричной форме
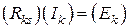 , (4.3)
, (4.3)
где 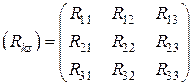 - квадратная симметричная матрица сопротивлений, количество строк и столбцов которой равняется n;
- квадратная симметричная матрица сопротивлений, количество строк и столбцов которой равняется n;
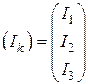 ;
; 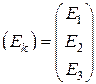 - матрицы контурных токов и ЭДС соответственно.
- матрицы контурных токов и ЭДС соответственно.
Итак, МКТ разрешает решить задачу Анализа цепи с количеством уравнений n = N - M +1.Найдем с (4.2) первый контурный ток
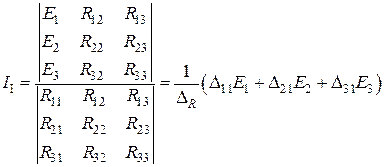 ,
,
где 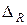 ,
, 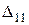 ,
, 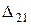 ,
, 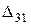 - определитель и алгебраические дополнение матрицы ребер.
- определитель и алгебраические дополнение матрицы ребер.
Аналогично можно найти любой (m-и) контурный ток в схеме:
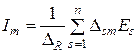 , (4.4)
, (4.4)
где n = N - M +1 - количество независимых контуров; m = 1,..., n; s = 1,..., n;
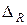 ,
, 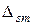 - определитель и алгебраические дополнение матрицы ребер;
- определитель и алгебраические дополнение матрицы ребер;
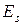 - элемент матрицы-столбца контурных ЭДС.
- элемент матрицы-столбца контурных ЭДС.
Токи внутренних веток определяются как линейная комбинация контурных токов. Для схемы (рис.4.1) 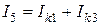 ;
; 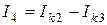 ;
; 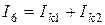 .
.
Распределение токов и напряжений в электрической цепи не изменится, если один из узлов (любой) заземлить, т.е. сделать его потенциал нулевым.
Базисным носит название узел, потенциал которого равняется нулю. Напряжения других узлов схемы, которые отсчитываются относительно базисного узла, носят название узловых напряжений. Принято узловые напряжения направлять к точке заземления (рис.4.2a). Ток в ветке, которая соединяет узел с базисным узлом, определяется по закону Ома: 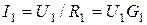 ;
; 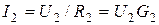 . Напряжение
. Напряжение 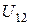 между узлами, ни один из которых не являются базисными, определяется по второму закону Кирхгофа (рис.4.2б):
между узлами, ни один из которых не являются базисными, определяется по второму закону Кирхгофа (рис.4.2б): 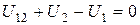 ;
; 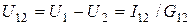 .
.
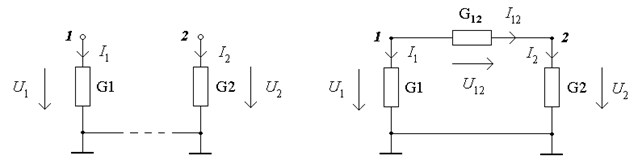
а) б)
Анализируя электрический круг по методу МУН необходимо провести эквивалентную замену источников ЭДС источниками тока. Проведем такую замену для электрического цепи (рис.4.1). Обозначим токи источников 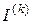 , а токи в ветках -
, а токи в ветках - 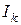 (рис.4.3).
(рис.4.3).
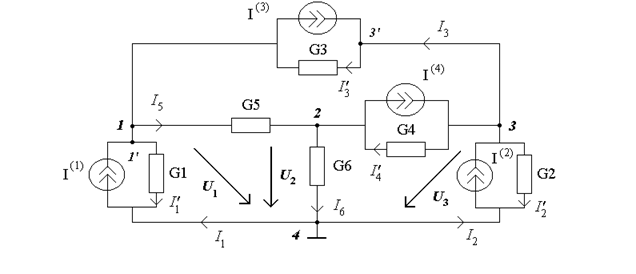
Изберем как базисный узел 4, и запишем по первому закону Кирхгофа уравнения для узла 1:
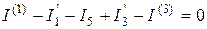 , (4.5)
, (4.5)
или 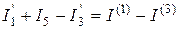 .
.
Воспользуемся законом Ома и выразим токи через узловые напряжения:
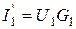 ;
; 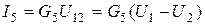 ;
; 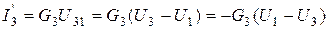 .
.
Подставив эти значения к последнему уравнения, будем иметь
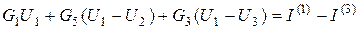 ;
;
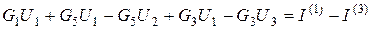 .
.
Сгруппировав слагаемые, запишем
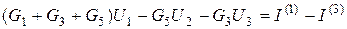 . (4.6)
. (4.6)
Обозначим 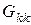 - собственная проводимость k -го узла, - которая равняется сумме проводимостей веток, близлежащих к k -му узлу (
- собственная проводимость k -го узла, - которая равняется сумме проводимостей веток, близлежащих к k -му узлу (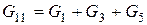 ,
, 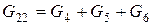 ,
, 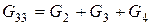 );
);
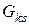 - взаимная проводимость k -го и s -го узлов, - которая равняется сумме проводимостей веток, что соединяют эти узлы, со знаком "минус" (
- взаимная проводимость k -го и s -го узлов, - которая равняется сумме проводимостей веток, что соединяют эти узлы, со знаком "минус" (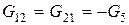 ,
, 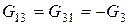 ;
; 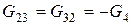 );
);
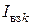 - узловой ток (любого) k -го узла, который равняется алгебраической сумме токов независимых источников, которые сходятся в k-м узле (
- узловой ток (любого) k -го узла, который равняется алгебраической сумме токов независимых источников, которые сходятся в k-м узле (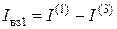 ,
, 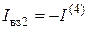 ,
, 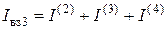 ). Токи источников, которые втекают в узел (вытекают из узла) входят в узловой ток
). Токи источников, которые втекают в узел (вытекают из узла) входят в узловой ток  со знаком «плюс» (со знаком «минус»).
со знаком «плюс» (со знаком «минус»).
Учитывая эти обозначения, запишем уравнения (4.6) в виде:
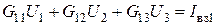 .
.
Записав аналогичные уравнения для узлов 2 и 3, получаем систему:
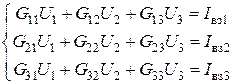 . (4.7)
. (4.7)
или в матричной форме
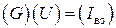 ,
,
где 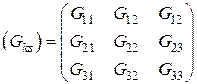 ,
, 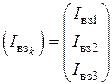 ,
, 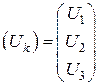 - матрицы проводимостей, узловых токов и узловых напряжений, соответственно.
- матрицы проводимостей, узловых токов и узловых напряжений, соответственно.
Определим из системы (4.7) узловое напряжение 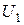 :
:
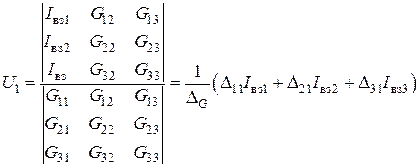 .
.
Аналогично получаем узловое напряжение любого узла по формуле
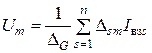 , (4.8)
, (4.8)
где 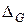 ,
,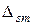 - определитель и алгебраические дополнение матрицы проводимостей [ G ]; n = M -1 - количество независимых узлов; m = 1,..., n; s = 1,..., n.
- определитель и алгебраические дополнение матрицы проводимостей [ G ]; n = M -1 - количество независимых узлов; m = 1,..., n; s = 1,..., n.
Напряжения на проводимостях, которые не соединенные с базисным узлом, определяются как линейная комбинация узловых напряжений. Для схемы (рис.4.3)
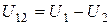 ;
; 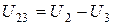 ;
; 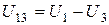 .
.
Токи веток определяются по закону Ома: 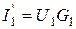 ;
; 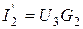 ;
; 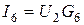 ;
; 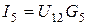 ;
; 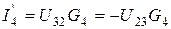 ;
; 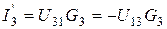 .
.
Токи веток выходной схемы (рис.4.1) 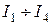 , определяются по первому закону Кирхгофа с учетом избранных направлений. Например, для узла 1' (рис.4.3) имеем:
, определяются по первому закону Кирхгофа с учетом избранных направлений. Например, для узла 1' (рис.4.3) имеем: 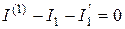 , откуда
, откуда 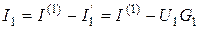 ; для узла 3':
; для узла 3': 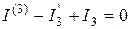 , откуда
, откуда 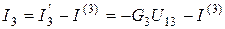 , и т.п..
, и т.п..
Пример. Для схемы (рис.4.4) по методу МКТ найти ток 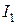 , если
, если 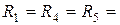 1 ком;
1 ком; 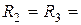 2 ком;
2 ком; 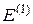 = 1 В;
= 1 В; 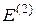 = 4 В,
= 4 В, 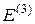 = 2 В.
= 2 В.
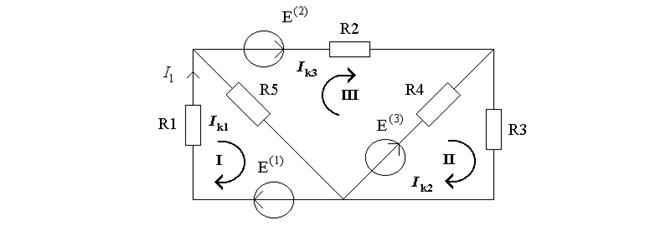
Обозначив контуры и избрав их обход по часовой стрелке, запишем матрицы (Rks) и (Ek):
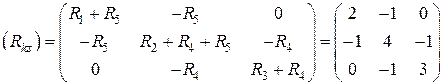 ;
; 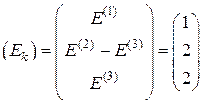 .
.
По формуле (4.4) определяем первый контурный ток, который будет одновременно и током в ветке 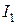 .
.
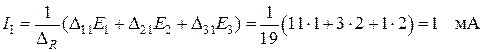 .
.
Свойства линейных электрических цепей, которые являются общими для цепей любой сложности, сформулированы в теоремах и упрощают задачу анализа цепи.
5.1 Входные и выходные сопротивления и проводимости
В предыдущей лекции были получены формулы для расчета контурных токов и узловых напряжений:
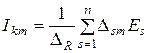 ,
, 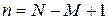 ;
; 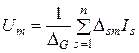 ,
, 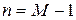 .
.
Пусть к какой-то ветке контура электрической цепи подключен независимый источник ЭДС  (рис.5.1а), причем эта ветка не является общей, а принадлежит только контуру m (независимое - это такой источник, ЭДС которого не зависит от всех других токов и напряжений электрической цепи).
(рис.5.1а), причем эта ветка не является общей, а принадлежит только контуру m (независимое - это такой источник, ЭДС которого не зависит от всех других токов и напряжений электрической цепи).
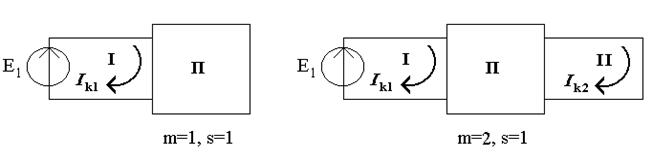
а) б)
в) г)
Рисунок 5.1
Если другая часть электрической цепи не имеет независимых источников электрической энергии, то по формуле (4.4) предоставленная ЭДС  вызовет в данном контуре (m =1, s =1) ток
вызовет в данном контуре (m =1, s =1) ток
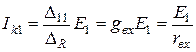 ,
,
где 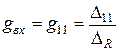 - входная проводимость,
- входная проводимость, 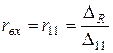 - входное сопротивление.
- входное сопротивление.
Итак, входная проводимость m -го контура
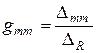 - (5.1)
- (5.1)
это отношение m -го контурного тока к ЭДС, которая действует в этом контуре при отсутствии источников в других контурах. Она показывает, какой именно ток в m -м контуре вызовет единая ЭДС, которая равняется 1 В, которая подключена к этому контуру.
В случае m =2, s =1 (рис.5.1б) предоставленная ЭДС 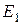 вызовет в контуре 2 ток
вызовет в контуре 2 ток
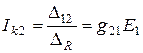 ,
,
где 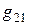 - передаточная проводимость 1- го и 2- го контуров.
- передаточная проводимость 1- го и 2- го контуров.
Итак, передаточная проводимость m -го и s -го контуров
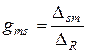 (5.2)
(5.2)
показывает, какой именно ток вызовет в m -м контуре единая ЭДС, которая равняется 1 В, которая подключена к s -го контуру (индекс m указывает ток, который определяется). Передаточная проводимость также может быть найденна по формуле
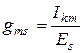 ;
; 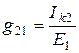 .
.
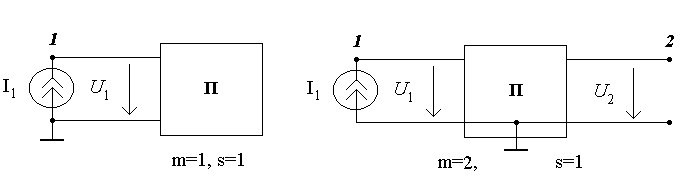
Аналогичные рассуждения касаются также относительно узлов m и s, если предположить, что к узлу m подключен независимый источник тока 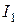 , а другая часть схемы не содержит независимых источников (рис.5.1в). Соответственно к (4.8), узловой ток
, а другая часть схемы не содержит независимых источников (рис.5.1в). Соответственно к (4.8), узловой ток 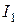 обусловит появление узловых напряжений для узла m:
обусловит появление узловых напряжений для узла m:
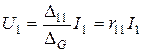 ,
,
где 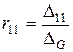 - входное сопротивление первого узла (m =1, s =1).
- входное сопротивление первого узла (m =1, s =1).
Для схемы (рис.5.1г) s =1 - узел, к которому включен источник тока, m =2 - узел, узловое напряжение которого определяем:
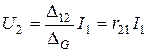 ,
,
где 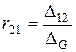 - передаточное сопротивление первого и второго узлов.
- передаточное сопротивление первого и второго узлов.
Итак, входное сопротивление m -го узла
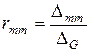 (5.3)
(5.3)
показывает, какое именно узловое напряжение узла m вызовет единый источник тока величиной 1 А, которій подключен между m -м и базисным узлами.
Передаточное сопротивление m -го и s -го узлов
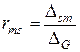 (5.4)
(5.4)
показывает, какое именно узловое напряжение вызовет единый источник тока величиной 1 А, которое питает только s -ий узел.
Заметим, что входным сопротивлением может также называться величина, обратная к выражению (5.1), а входной проводимостью - величина, обратная к (5.3). Очевидно, что для одной и той же пары зажимов электрической цепи, которая не содержит источников электрической энергии, 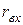 и
и 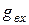 является взаимно обратными:
является взаимно обратными: 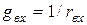 .
.
5.2 Теорема обратимости (взаемкости)
Пассивные линейные электрические цепи имеют важное свойство, которое известно под названием обратимость. Теорема обратимости, которая базируется на этом свойстве, может быть сформулированна в двух вариантах: относительно источников ЭДС и тока. Ограничимся рассмотрением первого варианта.
Введем такие понятия: внесение источника к электрической цепи носит название возбуждения или влияния; появление тока (напряжения) в цепи носит название реакции или отклика.
На рис.5.2 условно показана электрическая цепь с выделенными контурами 1 и 2. Для первой схемы 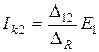 ; для второй -
; для второй - 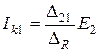 . Если
. Если 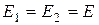 , можно записать
, можно записать
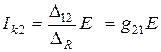 ;
; 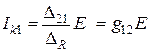 .
.
Матрица 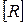 - симметричная, поэтому
- симметричная, поэтому 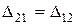 ,
, 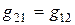 ,
, 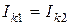 .
.
а) б)
 2014-02-09
2014-02-09 1327
1327








